题目内容
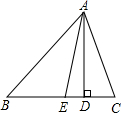 如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.
如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.分析:由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=
∠BAC,故∠DAE=∠EAC-∠DAC.
| 1 |
| 2 |
解答:解:∵∠B=36°,∠C=76°,
∴∠BAC=180°-∠B-∠C=68°,
∵AE是角平分线,
∴∠EAC=
∠BAC=34°.
∵AD是高,∠C=76°,
∴∠DAC=90°-∠C=14°,
∴∠DAE=∠EAC-∠DAC=34°-14°=20°.
∴∠BAC=180°-∠B-∠C=68°,
∵AE是角平分线,
∴∠EAC=
| 1 |
| 2 |
∵AD是高,∠C=76°,
∴∠DAC=90°-∠C=14°,
∴∠DAE=∠EAC-∠DAC=34°-14°=20°.
点评:本题主要考查了三角形内角和定理、角的平分线的性质、直角三角形的性质,比较综合,难度适中.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
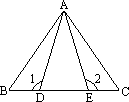
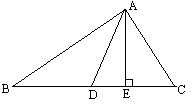
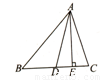
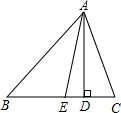 如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.
如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.