题目内容
【题目】如图1,已知一次函数y=ax+2与x轴、y轴分别交于点A,B,反比例函数y= ![]() 经过点M.
经过点M.
(1)若M是线段AB上的一个动点(不与点A、B重合).当a=﹣3时,设点M的横坐标为m,求k与m之间的函数关系式.
(2)当一次函数y=ax+2的图象与反比例函数y= ![]() 的图象有唯一公共点M,且OM=
的图象有唯一公共点M,且OM= ![]() ,求a的值.
,求a的值.
(3)当a=﹣2时,将Rt△AOB在第一象限内沿直线y=x平移 ![]() 个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
个单位长度得到Rt△A′O′B′,如图2,M是Rt△A′O′B′斜边上的一个动点,求k的取值范围.
【答案】
(1)解:当a=﹣3时,y=﹣3x+2,
当y=0时,﹣3x+2=0,
x= ![]() ,
,
∵点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合),
∴0<m< ![]() ,,DANG
,,DANG
则 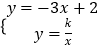 ,
,
﹣3x+2= ![]() ,
,
当x=m时,﹣3m+2= ![]() ,
,
∴k=﹣3m2+2m(0<m< ![]() )
)
(2)解:由题意得: 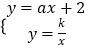 ,
,
ax+2= ![]() ,
,
ax2+2x﹣k=0,
∵直线y=ax+2(a≠0)与双曲线y= ![]() 有唯一公共点M时,
有唯一公共点M时,
∴△=4+4ak=0,
ak=﹣1,
∴k=﹣ ![]() ,
,
则 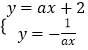 ,
,
解得: 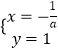 ,
,
∵OM= ![]() ,
,
∴12+(﹣ ![]() )2=(
)2=( ![]() )2,
)2,
a=± ![]()
(3)解:当a=﹣2时,y=﹣2x+2,
∴点A的坐标为(1,0),点B的坐标为(0,2),
∵将Rt△AOB在第一象限内沿直线y=x平移 ![]() 个单位得到Rt△A′O′B′,
个单位得到Rt△A′O′B′,
∴A′(2,1),B′(1,3),
点M是Rt△A′O′B′斜边上一动点,
当点M′与A′重合时,k=2,
当点M′与B′重合时,k=3,
∴k的取值范围是2≤k≤3
【解析】(1)当a=﹣3时,直线解析式为y=﹣3x+2,求出A点的横坐标,由于点M的横坐标为m,且M是线段AB上的一个动点(不与点A、B重合)从而得到m的取值范围,由﹣3x+2= ![]() ,由X=m得k=﹣3m2+2m(0<m<
,由X=m得k=﹣3m2+2m(0<m< ![]() );(2)由ax+2=
);(2)由ax+2= ![]() 得ax2+2x﹣k=0,直线y=ax+2(a≠0)与双曲线y=
得ax2+2x﹣k=0,直线y=ax+2(a≠0)与双曲线y= ![]() 有唯一公共点M时,△=4+4ak=0,ak=﹣1,由勾股定理即可;(3)当a=﹣2时,y=﹣2x+2,从而求出A、B两点的坐标,由平移的知识知A′,B′点的坐标,从而得到k的取值范围。
有唯一公共点M时,△=4+4ak=0,ak=﹣1,由勾股定理即可;(3)当a=﹣2时,y=﹣2x+2,从而求出A、B两点的坐标,由平移的知识知A′,B′点的坐标,从而得到k的取值范围。

 阅读快车系列答案
阅读快车系列答案





