题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转角
旋转角![]() 得
得![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
![]() 在旋转过程中,线段
在旋转过程中,线段![]() 与
与![]() 有怎样的数量关系?证明你的结论;
有怎样的数量关系?证明你的结论;
![]() 当
当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 在
在![]() 的情况下,求线段
的情况下,求线段![]() 的长.
的长.

【答案】(1)![]() .理由见解析;
.理由见解析;![]() 四边形
四边形![]() 是菱形.理由见解析;
是菱形.理由见解析;![]() .
.
【解析】
(1)根据等边对等角的性质可得∠A=∠C,再根据旋转的性质可得∠ABE=∠C1BF,AB=BC=A1B=BC1,然后利用“角边角”证明△ABE和△C1BF全等,根据全等三角形对应边相等可得BE=BF,从而得解;
(2)先根据旋转的性质求出∠ABC1=150°,再根据同旁内角互补,两直线平行求出AB∥C1D,AD∥BC1,证明四边形BC1DA是平行四边形,又因为邻边相等,所以四边形BC1DA是菱形;
(3)过点E作EG⊥AB于点G,等腰三角形三线合一的性质可得AG=BG=2,然后解直角三角形求出AE的长度,再利用DE=AD-AE计算即可得解.
(1)![]() .理由如下:
.理由如下:
∵![]() ,
,
∴![]() ,
,
∵![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得
得![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
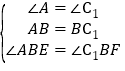 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
![]() 四边形
四边形![]() 是菱形.理由如下:
是菱形.理由如下:
∵旋转角![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形;
是菱形;
![]() 过点
过点![]() 作
作![]() ,
,

∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
由![]() 知
知![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A. 中位数是50 B. 众数是51 C. 方差是42 D. 极差是21




