Question

【题目】如图，在直角坐标平面内，△ABC的三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．

（1）填空：∠ ABC＝　 　，S△ABC＝　 　；

（2）画出△ABC关于x轴的对称图形△A1B1C1，再画出△A1B1C1关于y轴的对称图形△A2B2C2,在x轴上作一点p,使p到A,C两点间的距离和最短；

（3）若M是△ABC内一点，其坐标是（a，b），则△A2B2C2中，点M的对应点的坐标为　 　．

Answer 1

【答案】（1）∠ ABC＝45°；S△ABC＝；（2）见解析；（3）（﹣a，﹣b）

【解析】

（1）利用勾股定理求三角形三边的长，从而判定三角形形状，∠ ABC＝45°，在网格图中利用割补法求面积；（2）利用轴对称变换描点画出相应图形，然后根据轴对称及两点之间线段最短的知识，确定点P的位置；（3）根据题意可知△A2B2C2与△ABC关于原点对称，从而求解.

解：（1）∵A（0，3），B（3，4），C（2，2）

∴;;

∴△ABC为等腰直角三角形

∴∠ ABC＝45°；

S△ABC＝2×3﹣×1×3﹣×1×2×2＝；

(2)如图所示，△A1B1C1，△A2B2C2即为所求；连接A1C,交x轴于点P，点P即为所求；

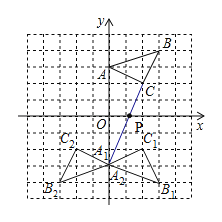
（3）由题意可知△A2B2C2与△ABC关于原点对称

∴点M的对应点的坐标为（﹣a，﹣b）．