题目内容
【题目】如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.
(1)如图1,求证:∠DAC=∠PAC;
(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,![]() ,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
,连接EF,过点F作AD的平行线交PC于点G,求证:FG=DE+DG;
(3)在(2)的条件下,如图3,若AE=![]() DG,PO=5,求EF的长.
DG,PO=5,求EF的长.

【答案】(1)证明见解析;(2)证明见解析;(3)EF=3![]() .
.
【解析】
(1)连接OC,求出OC∥AD,求出OC⊥PC,根据切线的判定推出即可;
(2)连接BE交GF于H,连接OH,求出四边形HGDE是矩形,求出DE=HG,FH=EH,即可得出答案;
(3)设OC交HE于M,连接OE、OF,求出∠FHO=∠EHO=45°,根据矩形的性质得出EH∥DG,求出OM=![]() AE,设OM=a,则HM=a,AE=2a,AE=
AE,设OM=a,则HM=a,AE=2a,AE=![]() DG,DG=3a,
DG,DG=3a,
求出ME=CD=2a,BM=2a,解直角三角形得出tan∠MBO=![]() ,tanP=
,tanP=![]() ,设OC=k,则PC=2k,根据OP=
,设OC=k,则PC=2k,根据OP=![]() k=5求出k=
k=5求出k=![]() ,根据勾股定理求出a,即可求出答案.
,根据勾股定理求出a,即可求出答案.
(1)证明:连接OC,
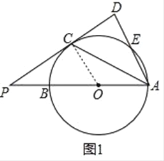
∵PC为⊙O的切线,
∴OC⊥PC,
∵AD⊥PC,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OC=OA,
∴∠PAC=∠OCA,
∴∠DAC=∠PAC;
(2)证明:连接BE交GF于H,连接OH,
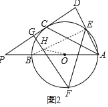
∵FG∥AD,
∴∠FGD+∠D=180°,
∵∠D=90°,
∴∠FGD=90°,
∵AB为⊙O的直径,
∴∠BEA=90°,
∴∠BED=90°,
∴∠D=∠HGD=∠BED=90°,
∴四边形HGDE是矩形,
∴DE=GH,DG=HE,∠GHE=90°,
∵![]() ,
,
∴∠HEF=∠FEA=![]() ∠BEA=
∠BEA=![]() =45°,
=45°,
∴∠HFE=90°﹣∠HEF=45°,
∴∠HEF=∠HFE,
∴FH=EH,
∴FG=FH+GH=DE+DG;
(3)解:设OC交HE于M,连接OE、OF,
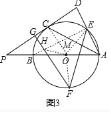
∵EH=HF,OE=OF,HO=HO,
∴△FHO≌△EHO,
∴∠FHO=∠EHO=45°,
∵四边形GHED是矩形,
∴EH∥DG,
∴∠OMH=∠OCP=90°,
∴∠HOM=90°﹣∠OHM=90°﹣45°=45°,
∴∠HOM=∠OHM,
∴HM=MO,
∵OM⊥BE,
∴BM=ME,
∴OM=![]() AE,
AE,
设OM=a,则HM=a,AE=2a,AE=![]() DG,DG=3a,
DG,DG=3a,
∵∠HGC=∠GCM=∠GHE=90°,
∴四边形GHMC是矩形,
∴GC=HM=a,DC=DG﹣GC=2a,
∵DG=HE,GC=HM,
∴ME=CD=2a,BM=2a,
在Rt△BOM中,tan∠MBO=![]() ,
,
∵EH∥DP,
∴∠P=∠MBO,
tanP=![]() ,
,
设OC=k,则PC=2k,
在Rt△POC中,OP=![]() k=5,
k=5,
解得:k=![]() ,OE=OC=
,OE=OC=![]() ,
,
在Rt△OME中,OM2+ME2=OE2,5a2=5,
a=1,
∴HE=3a=3,
在Rt△HFE中,∠HEF=45°,
∴EF=![]() HE=3
HE=3![]() .
.







