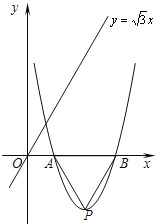题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2﹣(3m+1)x+2m2+m(m>0),与y轴交于点C,与x轴交于点A(x1,0),B(x2,0),且x1<x2.
(1)求2x1﹣x2+3的值;
(2)当m=2x1﹣x2+3时,将此抛物线沿对称轴向上平移n个单位,使平移后得到的抛物线顶点落在△ABC的内部(不包括△ABC的边),求n的取值范围(直接写出答案即可).
【答案】(1)2;(2)![]() <n<
<n<![]() .
.
【解析】
(1)解关于x的一元二次方程x2﹣(3m+1)x+2m2+m=0,结合已知条件可求得x1、x2的值,然后代入2x1﹣x2+3进行计算即可得;
(2)由(1)可知m=2,继而可得抛物线解析式为y=x2﹣7x+10,A(2,0),B(5,0),C(0,10),通过配方可求得抛物线的顶点坐标以及对称轴,由B、C坐标易得直线BC的解析式为y=﹣2x+10,继而可得直线BC与抛物线的对称轴的交点为(![]() ,3),继而可求得n的取值范围.
,3),继而可求得n的取值范围.
(1)解关于x的一元二次方程x2﹣(3m+1)x+2m2+m=0,得x=2m+1或x=m,
∵m>0,x1<x2,
∴x1=m,x2=2m+1,
∴2x1﹣x2+3=2m﹣2m﹣1+3=2;
(2)当m=2时,抛物线解析式为y=x2﹣7x+10,A(2,0),B(5,0),C(0,10),
∵y=x2﹣7x+10=(x﹣![]() )2﹣
)2﹣![]() ,
,
∴抛物线的顶点坐标为(![]() ,﹣
,﹣![]() ),抛物线的对称轴为直线x=
),抛物线的对称轴为直线x=![]() ,
,
易得直线BC的解析式为y=﹣2x+10,
当x=![]() 时,y=﹣2x+10=3,则n=
时,y=﹣2x+10=3,则n=![]() ,
,
∴将此抛物线沿对称轴向上平移n个单位,使平移后得到的抛物线顶点落在△ABC的内部(不包括△ABC的边)时,n的取值范围是![]() <n<
<n<![]() .
.

练习册系列答案
相关题目