Question

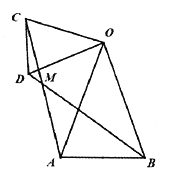
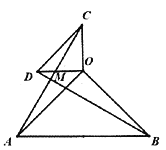
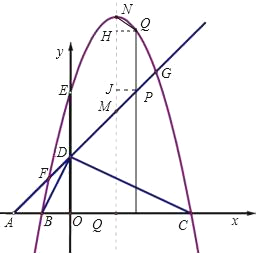
【题目】如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

（1）求经过B、E、C三点的抛物线的解析式；

（2）判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

（3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．

Answer 1

【答案】（1）y=﹣x2+3x+4；（2）△BDC是直角三角形，证明见解析；△POC是等腰三角形时，点P坐标是（﹣1+，1+）或（2，4）；（3）①不能成为菱形，理由见解析；②能成为等腰梯形，点P的坐标是（2.5，4.5）．

【解析】

(1)利用待定系数法列方程组求二次函数的解析式.(2)利用勾股定理的逆定理，判断直角三角形.(3)分别设出P，Q点坐标，按照菱形的条件，等腰梯形的条件，分别求P点坐标，判断是否存在.

（1）B（﹣1，0）E（0，4）C（4，0）设解析式是y=ax2+bx+c，

可得,

解得,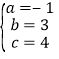

∴y=﹣x2+3x+4；

（2）△BDC是直角三角形，

∵BD2=BO2+DO2=5，DC2=DO2+CO2=20，BC2=（BO+CO）2=25

∴BD2+DC2=BC2，

∴△BDC是直角三角形．

点A坐标是（﹣2，0），点D坐标是（0，2），

设直线AD的解析式是y=kx+b，则,

解得：,

则直线AD的解析式是y=x+2，

设点P坐标是（x，x+2）

当OP=OC时x2+（x+2）2=16，

解得：x=﹣1±（x=﹣1-（不符合，舍去）此时点P（﹣1+，1+）

当PC=OC时（x+2）2+（4﹣x）2=16，方程无解；

当PO=PC时，点P在OC的中垂线上，

∴点P横坐标是2，得点P坐标是（2，4）；

∴当△POC是等腰三角形时，点P坐标是（﹣1+，1+）或（2，4）；

（3）点M坐标是（,），点N坐标是（,），∴MN=，

设点P为（x，x+2），Q（x，﹣x2+3x+4），则PQ=﹣x2+2x+2

①若PQNM是菱形，则PQ=MN，可得x1=0.5，x2=1.5

当x2=1.5时，点P与点M重合；当x1=0.5时，可求得PM=所以菱形不存在．

②能成为等腰梯形，作QH⊥MN于点H，作PJ⊥MN于点J，则NH=MJ，

则﹣（﹣x2+3x+4）=x+2﹣，

解得：x=2.5，

此时点P的坐标是（2.5，4.5）．