题目内容
【题目】(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
①求证:OE=BE.
②若△ABC的周长是25,BC=9,试求出△AEF的周长.
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=80°,∠PAC的度数?

【答案】(1)①见解析,②16;(2)50°
【解析】
(1)①由角平分线的性质、等腰三角形的性质和平行线的性质即可得到结论;②根据三角形的周长公式即可得到结论;
(2)延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,根据角平分线的性质先证的PF=PM,得出∠FAP=∠PAC即可得出答案.
(1)①∵BO平分∠ABC
∴∠EBO=∠OBC
∵EF∥BC
∴∠EOB=∠OBC
∴∠EOB=∠EBO
∴OE=BE;
②同理可得:OF=FC
∵△ABC的周长是25,BC=9
∴△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25-9=16;
(2)延长BA,做PN⊥BD,PF⊥BA,PM⊥AC,如图所示:
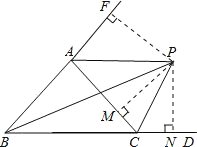
∵CP平分∠ACD,
∴PM=PN,
∵BP平分∠ABC,
∴PF=PN,
∴PF=PM,
∴∠FAP=∠PAC,
∴∠FAC=2∠PAC,
∵∠FAC+∠BAC=180°,
∴2∠PAC+∠BAC=180°
∴2∠PAC+80°=180°
∴∠PAC=50°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目











