题目内容
【题目】如图,点B,C,D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2 ![]() .
.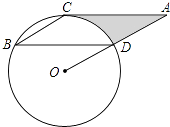
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
【答案】
(1)证明:连接OC,交BD于E,
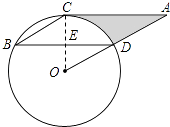
∵∠B=30°,∠B= ![]() ∠COD,
∠COD,
∴∠COD=60°,
∵∠A=30°,
∴∠OCA=90°,
即OC⊥AC,
∴AC是⊙O的切线
(2)解:∵AC∥BD,∠OCA=90°,
∴∠OED=∠OCA=90°,
∴DE= ![]() BD=
BD= ![]() ,
,
∵sin∠COD= ![]() ,
,
∴OD=2,
在Rt△ACO中,tan∠COA= ![]() ,
,
∴AC=2 ![]() ,
,
∴S阴影= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]()
【解析】(1)要证AC是⊙O的切线,连接OC,根据圆周角定理,可得出∠COD=60°,再证明OC⊥AC即可;
(2)由图可知S阴影=SRt△OAC-S△OCD,求出两个三角形的面积,就可以求出阴影部分的面积。

练习册系列答案
相关题目
【题目】我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
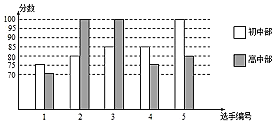
(1)根据所给信息填空:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
初中部 | 85 | ______ | 85 | _______ |
高中部 | _____ | 80 | ______ | 160 |
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.