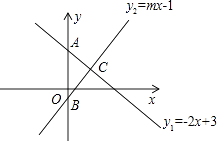题目内容
【题目】如图,已知一次函数![]() 与反比例函数
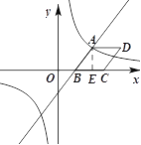
与反比例函数![]() 的图象在第一象限相交于点A(6,n),与x轴相交于点B.
的图象在第一象限相交于点A(6,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;当y2≥-4时,x的取值范围是 ;
(2)以AB为边作菱形ABCD,使点C在点B右侧的x轴上,求点D的坐标.

【答案】(1)n=4,k=24,x≤-6或x>0;(2)点D的坐标为(11,4).
【解析】(1)把点A(6,n)代入一次函数y=![]() x-4,得到n的值为4;再把点A(6,4)代入反比例函数y=
x-4,得到n的值为4;再把点A(6,4)代入反比例函数y=![]() ,得到k的值为24;根据反比例函数的性质即可得到y≥-4时,自变量x的取值范围;
,得到k的值为24;根据反比例函数的性质即可得到y≥-4时,自变量x的取值范围;
(2)过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=5,根据菱形的性质得点D的坐标.
解:(1)把点A(6,n)代入一次函数y=![]() x-4,可得n=
x-4,可得n=![]() ×6-4=4;
×6-4=4;
把点A(6,4)代入反比例函数y=![]() ,可得4=
,可得4=![]() ,
,
解得k=24;
当y=-4时,-4=![]() ,解得x=-6.
,解得x=-6.
故当y≥-4时,自变量x 的取值范围是x≤-6或x>0.
(2)由![]() ,解得x=3
,解得x=3
∴B(3,0)
作AE⊥x轴于E,则E(6,0),AE=4,BE=3
在Rt△ABE中,
![]()
∵四边形ABCD是菱形,BC在x轴上,
∴AD=AB=5,AD∥x轴,
∴将点A向右移动5个单位长度得点D的坐标为(11,4).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目