题目内容
【题目】在Rt△ABC中,∠ACB=90°,点D为斜边AB的中点,BC=6,CD=5,过点A作AE⊥AD且AE=AD,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
【答案】![]() 或
或![]() .
.
【解析】
试题分析:分两种情况:①点E在CF上方,根据直角三角形的性质得出AC=8,作DG⊥AC可得AG=4、DG=3,再证△EAF≌△ADG可得AF=DG=3,即GF=7,由勾股定理即可得答案;②点E在AC下方时,与①同理可得.
试题解析:①如图1,当点E在CF上方时,∵点D为斜边AB的中点,BC=6,CD=5,∴CD=AD=DB=![]() AB=5,∴AB=10,AC=8,过点D作DG⊥AC于G,∴AG=CG=
AB=5,∴AB=10,AC=8,过点D作DG⊥AC于G,∴AG=CG=![]() AC=4,DG=
AC=4,DG=![]() BC=3,∠EFA=∠AGD=90°,∴∠EAF+∠AEF=90°,又∵AE⊥AD,∴∠EAF+∠DAG=90°,∴∠AEF=∠DAG,在△EAF和△ADG中,∵∠EFA=∠AGD,∠AEF=∠DAG,AE=AD,∴△EAF≌△ADG(AAS),∴AF=DG=3,∴在Rt△DFG中,DF=
BC=3,∠EFA=∠AGD=90°,∴∠EAF+∠AEF=90°,又∵AE⊥AD,∴∠EAF+∠DAG=90°,∴∠AEF=∠DAG,在△EAF和△ADG中,∵∠EFA=∠AGD,∠AEF=∠DAG,AE=AD,∴△EAF≌△ADG(AAS),∴AF=DG=3,∴在Rt△DFG中,DF=![]() =
=![]() =
=![]() ;
;

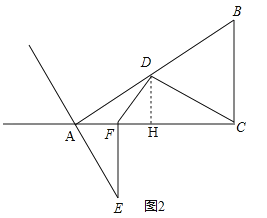
②如图2,当点E在AC下方时,作DH⊥AC于H,与①同理可得△DAH≌△AEF,∴AF=DH=3,∴FH=AH﹣AF=1,则DF=![]() =
=![]() =
=![]() ,综上,DF的长为
,综上,DF的长为![]() 或
或![]() .
.

练习册系列答案
相关题目