题目内容
【题目】已知:如图,∠AOB=70°,∠AOC=30°,OD平分∠BOC.请依题意补全图形,并求∠AOD的度数.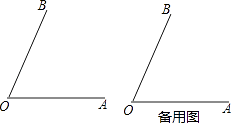
【答案】解:分两种情况进行讨论:
①如图1,射线OC在∠AOB的内部.

∵∠BOC=∠AOB﹣∠BOC,∠AOB=70°,∠AOC=30°,
∴∠BOC=70°﹣30°=40°.
又∵0D平分∠BOC,
∴∠COD=20°,
∴∠AOD=∠COD+∠AOC=50°;
②如图2,射线OC在∠AOB的外部.

∵∠BOC=∠AOB+∠BOC,∠AOB=70°,∠AOC=30°,
∴∠BOC=70°+30°=100°.
又∵0D平分∠BOC,
∴∠COD=50°,
∴∠AOD=∠COD﹣∠AOC=20°.
综上所述,∠AOD=50°或20°.
【解析】(1)根据题意画出图形;(2)分两种情况进行讨论,①射线OC在∠AOB的内部时,求出∠BOC=∠AOB﹣∠BOC的值,由OD平分∠BOC,根据角平分线定义,求出∠AOD=∠COD+∠AOC的值;②射线OC在∠AOB的外部时,求出∠BOC=∠AOB+∠BOC的值,由OD平分∠BOC,根据角平分线定义,求出∠AOD=∠COD﹣∠AOC的值.
【考点精析】根据题目的已知条件,利用角的平分线和角的比较的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;用量角器量出角的度数,角的大小按其度数比较(角的大小只与开口大小有关,与所画边的长短无关);角分为锐角、直角、钝角、平角、周角.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个,挂放在迎宾大道两侧,搭配每个造型所要花盆数如表,综合上述信息,解答下列问题.
造型 | 甲 | 乙 |
A | 90盆 | 30盆 |
B | 40盆 | 100盆 |
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个乙种造型的成本为1200元,选(1)中那种方案的成本最低?