题目内容
【题目】如图所示,已知∠A=∠F,∠C=∠D,按图填空,并在括号内注明理由.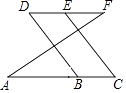
∵∠A=∠F()
∴∥()
∴∠D=∠ABD()
又∵∠D=∠C()
∴∠C=∠ABD()
∴∥()
【答案】已知;DF;AC;内错角相等,两直线平行;两直线平行,内错角相等;已知;等量代换;BD;EC;同位角相等,两直线平行
【解析】解:∵∠A=∠F(已知),
∴DF∥AC(内错角相等,两直线平行),
∴∠D=∠ABD(两直线平行,内错角相等),
∵∠D=∠C(已知),
∴∠C=∠ABD(等量代换),
∴BD∥EC(同位角相等,两直线平行),
所以答案是:已知,DF,AC,内错角相等,两直线平行,两直线平行,内错角相等,已知,等量代换,BD,EC,同位角相等,两直线平行.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

【题目】园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个,挂放在迎宾大道两侧,搭配每个造型所要花盆数如表,综合上述信息,解答下列问题.
造型 | 甲 | 乙 |
A | 90盆 | 30盆 |
B | 40盆 | 100盆 |
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A种造型的成本为1000元,搭配一个乙种造型的成本为1200元,选(1)中那种方案的成本最低?
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.