题目内容
【题目】解不等式组
请结合题意填空，完成本题的解答．
(Ⅰ)解不等式①，得_______________；
(Ⅱ)解不等式②，得_______________；
(Ⅲ)把不等式①和②的解集在数轴上表示出来；
(Ⅳ)原不等式组的解集为________________．
【答案】(Ⅰ)
；(Ⅱ)
；(Ⅲ)答案见解析；(Ⅳ)
．
【解析】
(Ⅰ)移项，合并同类项，把系数化“
”，可得结论；
(Ⅱ)去括号，移项，合并同类项，把系数化“”，可得结论；
(Ⅲ)在数轴上描出
，使用空心圈，画图时，大于向右，小于向左．
(Ⅳ)根据数轴，得出不等式组的解集即可．
解：(Ⅰ)由①得：
故答案为：；
(Ⅱ)由②得：
，
故答案为：；
(Ⅲ)把不等式①②的解集在数轴上表示如下：
(Ⅳ)根据数轴得到不等式组的解集为：
．
故答案为：．
暑假作业安徽少年儿童出版社系列答案
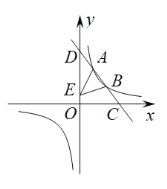
【题目】如图，在半
中，P是直径AB上一动点，且
，过点P作
交半于点C，P为垂足，连接BC，过点P作
于点D．
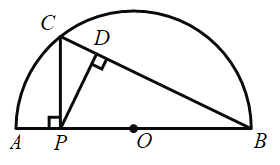
小明根据学习函数的经验，对线段AP，CP，PD的长度之间的关系进行了探究．下面是小明的探究过程，请补充完整：
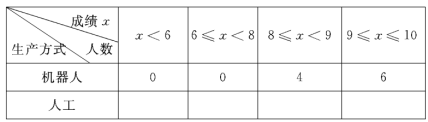
（1）对于动点P在AB上的不同位置，画图，测量，得到了线段AP，CP，PD的长度的几组值，如下表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | 位置10 | |
| 0.37 | 0.88 | 1.59 | 2.01 | 2.44 | 3.00 | 3.58 | 4.37 | 5.03 | 5.51 |
| 1.45 | 2.12 | 2.65 | 2.83 | 2.95 | 3.00 | 2.95 | 2.67 | 2.21 | 1.65 |
| 1.40 | 1.96 | 2.27 | 2.31 | 2.27 | 2.13 | 1.87 | 1.39 | 0.89 | 0.48 |
在AP，CP，PD的长度这三个量中，确定________的长度是自变量， ________的长度和________的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
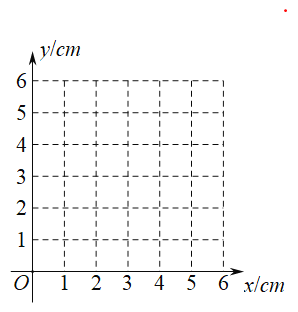
（3）结合函数图象，解决问题：当
时，AP的长度约为________．
