题目内容
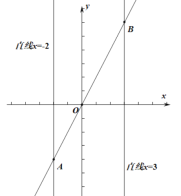
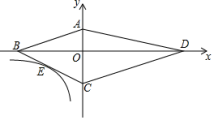
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(Ⅰ)当![]() 时,求二次函数的最大值;
时,求二次函数的最大值;
(Ⅱ)当![]() 时,点
时,点![]() 是
是![]() 轴上的点,
轴上的点,![]() ,将点
,将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,点
,点![]() 恰好落在该二次函数的图象上,求
恰好落在该二次函数的图象上,求![]() 的值;
的值;
(Ⅲ)![]() 是该二次函数图象上的一点,在(Ⅱ)的条件下,连接
是该二次函数图象上的一点,在(Ⅱ)的条件下,连接![]() ,
,![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(Ⅰ)12;(Ⅱ)![]() ;(Ⅲ)点
;(Ⅲ)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)将b=6代入求出函数解析式,通过配方后求出二次函数的最值;
(2)将b=2代入代入求出函数解析式,过点![]() 作
作![]() 轴于点
轴于点![]() ,证得
,证得![]() ,从而有EH=OP,从而求得
,从而有EH=OP,从而求得![]() ,将E点的坐标代入函数解析式,解方程即可求出t的值;(3)点M的位置不确定,需要进行分类讨论,分两种情况,点M在x轴上方和在x轴下方.
,将E点的坐标代入函数解析式,解方程即可求出t的值;(3)点M的位置不确定,需要进行分类讨论,分两种情况,点M在x轴上方和在x轴下方.
解:(Ⅰ)当![]() 时,
时,![]() ,∴二次函数的最大值为12;
,∴二次函数的最大值为12;
(Ⅱ)当![]() 时,
时,![]() ,
,
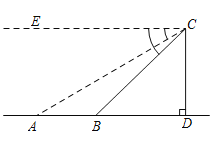
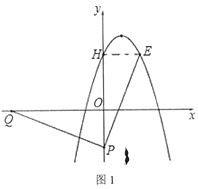
如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() .
.
∵将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() .
.
当点![]() 恰好在该二次函数的图象上时,有
恰好在该二次函数的图象上时,有![]() ,
,
解得![]() (舍去).
(舍去).
![]() .
.
(Ⅲ)设点![]() ,
,
①若点![]() 在
在![]() 轴上方,
轴上方,
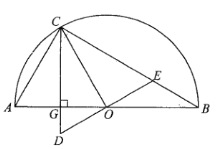
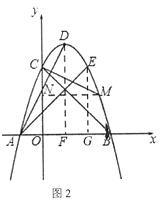
如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() .
.
![]() ,
,
令![]() ,则
,则![]() .
.
![]() .
.
令![]() ,则
,则![]() ,
,
解得![]() .
.
![]() .
.
![]() .
.
![]() .
.
由(Ⅱ)知![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,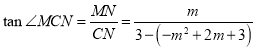 .
.
![]() .
.
解得![]() (舍去),
(舍去),![]() .
.
![]() .
.
②若点![]() 在
在![]() 轴下方,
轴下方,
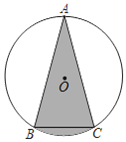
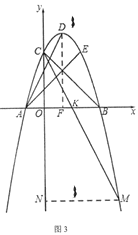
如图3,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() .
.
![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,
有![]() .
.
![]() 轴,
轴,
![]() .
.
![]() .
.
![]() ,
,
又![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() .
.
![]() .
.
解得![]() (舍去),
(舍去),![]() .
.
![]() .
.
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
【题目】意外创伤随时可能发生,急救是否及时、妥善,直接关系到病人的安危.为普及急救科普知识,提高学生的急救意识与现场急救能力,某校开展了急救知识进校园培训活动.为了解七、八年级学生(七、八年级各有600名学生)的培训效果,该校举行了相关的急救知识竞赛.现从两个年级各随机抽取20名学生的急救知识竞赛成绩(百.分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,78,81,72,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 | |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 | c |
八年级 | 78 | d | 80.5 |
应用数据:
(1)由上表填空:a= ;b= ;c= ;d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在80分及以上的共有多少人?
(3)你认为哪个年级的学生对急救知识掌握的总体水平较好,请说明理由.