题目内容
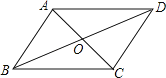
【题目】如图,在菱形ABCD中,tanA= ![]() ,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=
,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG= ![]() CG2;其中正确结论的序号为________.
CG2;其中正确结论的序号为________.
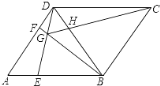
【答案】(1)(3)(4)
【解析】
(1)正确,先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;
(2)错误,只要证明△GDC≌△BGC,利用等腰三角形性质即可解决问题.
(3))正确,由△AED≌△DFB,推出∠ADE=∠DBF,所以∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,
(4)正确,证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积.
(1)∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
在△AED和△DFB中,AE=DF,∠A=∠BDF,AD=BD,
∴△AED≌△DFB,故本小题正确;
(2)当点E,F分别是AB,AD中点时,
由(1)知,△ABD,△BDC为等边三角形,
∵点E,F分别是AB,AD中点,
∴∠BDE=∠DBG=30°,
∴DG=BG,
在△GDC与△BGC中,DG=BG,CG=CGC,D=CB,
∴△GDC≌△BGC,
∴∠DCG=∠BCG,
∴CH⊥BD,即CG⊥BD,故本选项错误;
(3)∵△AED≌△DFB,
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,故本选项正确.
(4)∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B. C. D. G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.过点C作CM⊥GB于M,CN⊥GD于N.(如图2) 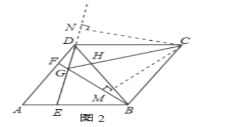
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=![]() CG,CM=
CG,CM=![]() CG,
CG,
∴S四边形CMGN=2S△CMG=2×![]() ×
×![]() CG×
CG×![]() CG=
CG=![]() CG2,故本小题正确.
CG2,故本小题正确.
综上所述,正确的结论有(1)(3)(4).
故答案为:(1)(3)(4).

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?