��Ŀ����
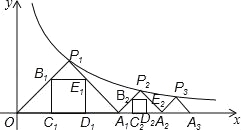
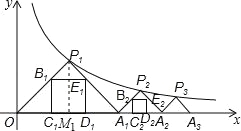
����Ŀ����ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���y=![]() ��x��0����ͼ���ϣ���P1OA����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA1���ڽ�������B1C1D1E1���ܳ���Ϊl1����P2A1A2���ڽ������ε��ܳ���Ϊl2��������PnAn��1An���ڽ�������BnCnDnEn���ܳ���Ϊln����l1+l2+l3+��+ln= ���ú�n��ʽ�ӱ�ʾ����
��x��0����ͼ���ϣ���P1OA����P2A1A2����P3A2A3��������PnAn��1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An��1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA1���ڽ�������B1C1D1E1���ܳ���Ϊl1����P2A1A2���ڽ������ε��ܳ���Ϊl2��������PnAn��1An���ڽ�������BnCnDnEn���ܳ���Ϊln����l1+l2+l3+��+ln= ���ú�n��ʽ�ӱ�ʾ����
���𰸡�![]()
![]()
��������
������������P1��P1M1��x����M1��
��֪M1��1��0����OA1���е㣬
��A1��2��0����
�ɵ�P1������Ϊ��1��1����
��P1O�Ľ���ʽΪ��y=x��
��P1O��A1P2����A1P2�ı���ʽһ����ϵ����ȣ�
��A1��2��0������y=x+b��
��b=��2��
��A1P2�ı���ʽ��y=x��2��
��y=![]() ��x��0�����������P2��1+
��x��0�����������P2��1+![]() ����1+
����1+![]() ����
����
���ϣ�A2��2![]() ��0����
��0����
P3��![]() +
+![]() ����
����![]() +
+![]() ����A3��2
����A3��2![]() ��0����
��0����
�������ƣ���An������Ϊ��2![]() ��0����
��0����
��l1=![]() OA1��l2=
OA1��l2=![]() A1A2��l3=
A1A2��l3=![]() A2A3��ln=
A2A3��ln=![]() An��1An��
An��1An��
��l1+l2+l3+��+ln=![]() OAn=
OAn=![]() ��2
��2![]() =
=![]()
![]() ��
��
�ʴ�Ϊ��![]()
![]() ��
��

 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�