��Ŀ����
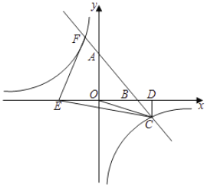
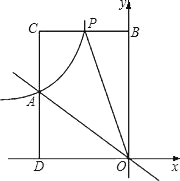
����Ŀ����ͼ��ʾ������������y��kx�뷴��������![]() ��ͼ���ڵ�A����3��2����
��ͼ���ڵ�A����3��2����
��1����ȷ�����������������뷴���������Ľ���ʽ��
��2������ͼ��ش��ڵڶ������ڣ���xȡ��ֵʱ��������������ֵ����������������ֵ��
��3��P��m��n���Ƿ���������ͼ���ϵ�һ���㣬���Щ�3��m��0������P��ֱ��PB��x�ᣬ��y���ڵ�B������A��ֱ��AD��y�ᣬ��x���ڵ�D����ֱ��PB�ڵ�C�����ı���OACP�����Ϊ6ʱ�����ж��߶�BP��CP�Ĵ�С��ϵ����˵�����ɣ�
���𰸡���1�������������뷴���������Ľ���ʽ�ֱ���y����![]() x��y����
x��y����![]() ����2����3��x��0����3���߶�BP��CP�Ĵ�С��ϵ��BP��CP.
����2����3��x��0����3���߶�BP��CP�Ĵ�С��ϵ��BP��CP.
��������
��1����A������������ʽ���k��m���ɣ�
��2������ͼ����ͼ��xȡ��ͬ����ʱy��ֵ��������𰸣�
��3�����mn��ֵ�����������ε������ʽ�õ�3n-![]() ��3��2-
��3��2-![]() ����-mn��=6�����m��n��ֵ�����BP��CP��ֵ���ɣ�
����-mn��=6�����m��n��ֵ�����BP��CP��ֵ���ɣ�
��1����A����3��2������y��kx�ã�2����3k��
��ã�k����![]() ��
��
��y����![]() x��
x��
����y��![]() �ã�m����6��
�ã�m����6��
��y����![]() ��
��
�������������뷴���������Ľ���ʽ�ֱ���y����![]() x��y����
x��y����![]() ��
��
��2����A����3��2����
��ͼ���֪������3��x��0ʱ���ڵڶ������ڣ�������������ֵ����������������ֵ��
��3�����߶�BP��CP�Ĵ�С��ϵ��BP��CP��
�����ǣ���P��m��n����y����![]() �ϣ�
�ϣ�
��mn����6��
��DO��3��AD��2��OB��n��BP����m��CP��3��PB��DC��n��
�ı���OACP�����Ϊ6��
��S����CDOB��S��ADO��S��OBP��6��
3n��![]() ��3��2��
��3��2��![]() ������mn����6��
������mn����6��
3n��3��![]() ��6��6��
��6��6��
3n��12��
��ã�n��4��
��m����![]() ��
��
��P����![]() ��4����
��4����
��PB��![]() ��CP��3��
��CP��3��![]() ��
��![]() ��
��
��BP��CP��