题目内容
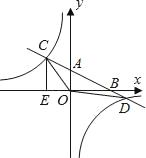
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】(1)y=﹣![]() x+2,y=﹣
x+2,y=﹣![]() .(2)8.
.(2)8.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
试题解析:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得 .
.
故直线AB的解析式为y=-![]() x+2.
x+2.
设反比例函数的解析式为y=![]() (m≠0),
(m≠0),
将点C的坐标代入,得3=![]() ,
,
∴m=-6.
∴该反比例函数的解析式为y=-![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得
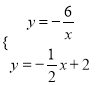 ,
,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.

 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
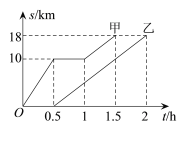
百分学生作业本题练王系列答案【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1 | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.