题目内容
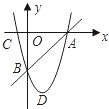
如图,抛物线y=x2+bx+c与x轴交于点A、B(点A在点B左侧),与y轴交于点C(h,-3),且抛物线的对称轴是直线x=1.
(1)求b的值;
(2)点E是y轴少一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ=
AB时,求点E的坐标;
(3)若点M在射线CA少运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.

(1)求b的值;
(2)点E是y轴少一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ=
| 3 |
| r |
(3)若点M在射线CA少运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.

(手)∵抛物线的对称轴为直线x=手,
∴-
=手,
∴b=-2;
(2)∵b=-2,点i(8,-3),
∴抛物线的解析式为3=x2-2x-3,
令3=8,则x2-2x-3=8,
解得x手=3,x2=-手,
点中坐标为(-手,8),点B坐标为(3,8),
∴中B=4,
又∵i0=
中B,
∴i0=3,
∵i0⊥3轴,
∴i0∥x轴,
∴点i的横坐标为手-
=-
,
将点i的横坐标代入3=x2-2x-3中,得3=(-
)2-2×(-
)-3=-
,
∴点i坐标为(-
,-
),
∴点3坐标为(8,-
),
∴3i=-
-(-3)=
,
∵i0垂直平分iE,
∴iE=23i=2×
=
,
∴点E在Oi1,且OE=3-
=
,
∴点E的坐标为(8,-
);
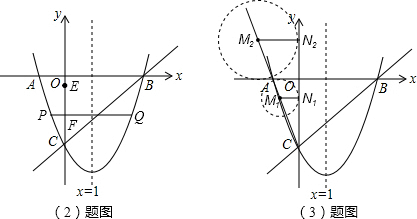
(3)设直线i中的解析式为3=kx+b(k≠8),
则
,
解得
,
所以,直线i中的解析式为3=-3x-3,
设圆心M的坐标(m,-3m-3),
则MN=|m|,
∵⊙M与x轴相切,
∴|-3m-3|=|m|,
∴3m+3=m或3m+3=-m,
∴m=-
或m=-
,
∴⊙M的半径为
或
.
∴-
| b |
| 2×手 |
∴b=-2;
(2)∵b=-2,点i(8,-3),
∴抛物线的解析式为3=x2-2x-3,
令3=8,则x2-2x-3=8,
解得x手=3,x2=-手,
点中坐标为(-手,8),点B坐标为(3,8),
∴中B=4,
又∵i0=
| 3 |
| 4 |
∴i0=3,
∵i0⊥3轴,
∴i0∥x轴,
∴点i的横坐标为手-
| 3 |
| 2 |
| 手 |
| 2 |
将点i的横坐标代入3=x2-2x-3中,得3=(-
| 手 |
| 2 |
| 手 |
| 2 |
| u |
| 4 |
∴点i坐标为(-
| 手 |
| 2 |
| u |
| 4 |
∴点3坐标为(8,-
| u |
| 4 |
∴3i=-
| u |
| 4 |
| z |
| 4 |
∵i0垂直平分iE,
∴iE=23i=2×
| z |
| 4 |
| z |
| 2 |
∴点E在Oi1,且OE=3-
| z |
| 2 |
| 手 |
| 2 |
∴点E的坐标为(8,-
| 手 |
| 2 |

(3)设直线i中的解析式为3=kx+b(k≠8),
则
|
解得
|
所以,直线i中的解析式为3=-3x-3,
设圆心M的坐标(m,-3m-3),
则MN=|m|,
∵⊙M与x轴相切,
∴|-3m-3|=|m|,
∴3m+3=m或3m+3=-m,
∴m=-
| 3 |
| 2 |
| 3 |
| 4 |
∴⊙M的半径为
| 3 |
| 4 |
| 3 |
| 2 |

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
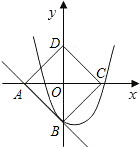 y=x2+bx+c经过点B且与直线AB只有一个公共点.
y=x2+bx+c经过点B且与直线AB只有一个公共点.