题目内容
【题目】已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A,B两点(点A在点B左侧),与y轴交于点C、设直线CM与x轴交于点D.
(1)求抛物线的解析式.
(2)在抛物线的对称轴上是否存在点P,使以点P为圆心的圆经过A、B两点,且与直线CD相切?若存在,求出P的坐标;若不存在.请说明理由.
(3)设直线y=kx+2与抛物线交于Q、R两点,若原点O在以QR为直径的圆外,请直接写出k的取值范围.
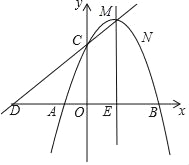
【答案】(1)y=﹣x2+2x+3;(2)满足题意的点P存在,其坐标为(1,﹣4+2![]() );(3)
);(3)![]() <k<
<k<![]() .
.
【解析】
(1)根据待定系数法即可解答.
(2) 假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u)其中u>0,得到PA2=u2+22,再利用已知条件即可解答.
(3) 设P(x1,y1),Q(x2,y2),PQ的中点为w,得出解析式进而求线段长度,即可解答.
(1)解:由抛物线的顶点是M(1,4),
设解析式为y=a(x﹣1)2+4(a<0),
又∵抛物线经过点N(2,3),
∴3=a(2﹣1)2+4,解得a=﹣1.
故所求抛物线的解析式为y=﹣(x﹣1)2+4,
即y=﹣x2+2x+3;
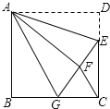
(2)解:如图:
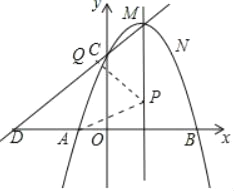
假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u)其中u>0,
则PA是圆的半径且PA2=u2+22,
过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切.
由题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u,PM=|4﹣u|,PQ=![]() PM.
PM.
由PQ2=PA2得方程:
![]() (4﹣u)2=u2+22,
(4﹣u)2=u2+22,
解得u=﹣4+2![]() ,u=﹣4﹣2
,u=﹣4﹣2![]() (不符合题意,舍).
(不符合题意,舍).
所以,满足题意的点P存在,其坐标为(1,﹣4+2![]() ).
).
(3)如图,设P(x1,y1),Q(x2,y2),PQ的中点为w.
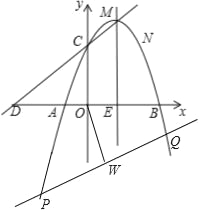
由![]() ,消去y得到:x2+(k﹣2)x﹣1=0,
,消去y得到:x2+(k﹣2)x﹣1=0,
∴x1+x2=2﹣k,x1x2=﹣1,
∴y1+y2=k(x1+x2)+4=﹣k2+2k+4,y1y2=k2(x1x2)+2k(x1+x2)+4=﹣3k2+4k+4,
∴W(![]() ,
,![]() ),
),
PQ=![]()
=![]()
∵原点O在以QR为直径的圆外,
∴2OW>PQ,
∴2![]() >
>![]()
整理得:3k2﹣4k﹣3<0,
解得![]() <k<
<k<![]() .
.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
【题目】有这样一个问题:探究函数y=![]() ﹣2x的图象与性质.
﹣2x的图象与性质.
小东根据学习函数的经验,对函数y=![]() ﹣2x的图象与性质进行了探究.
﹣2x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=![]() ﹣2x的自变量x的取值范围是_______;
﹣2x的自变量x的取值范围是_______;
(2)如表是y与x的几组对应值
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | m |
|
| … |
则m的值为_______;
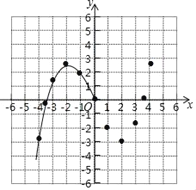
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)观察图象,写出该函数的两条性质________.