题目内容
【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx﹣8与x轴交于两点A，B，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为点D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（﹣2，0），（6，﹣8）．
（1）求抛物线的函数表达式；
（2）求点E的坐标；
（3）试探究在x轴下方的抛物线上是否存在点F，使得△FOB和△EOB的面积相等，若存在，请求出点F的坐标，若不存在，请说明理由；
（4）若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点Q，请直接写出：当m为何值时，△OPQ是等腰三角形．
【答案】
（1）
解：将点A（﹣2，0）、D（6，﹣8）代入y=ax2+bx﹣8，
得： 
，
解得：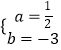 
，
∴抛物线的函数表达式为y= 
x2﹣3x﹣8
（2）
解：设直线l的解析式为y=kx，
将D（6，﹣8）代入，得：6k=﹣8，
解得：k=﹣ 
，
∴直线l的解析式为y=﹣ x，
又抛物线的对称轴为x=﹣ 
=3，
∴点E的坐标为（3，﹣4）
（3）
解：存在，
设点F（x， x2﹣3x﹣8），
∵S△FOB=S△EOB，即 OByF= OByE，
∴yF=yE，即 x2﹣3x﹣8=﹣4，
解得：x=3± 
，
∴点F的坐标为（3﹣ ，﹣4）或（3+ ，﹣4）
（4）
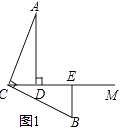
解：①如图1
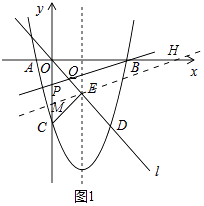
当OP=OQ时，△OPQ是等腰三角形．
∵点E坐标（3，﹣4），
∴OE= 
=5，过点E作直线ME∥PB，交y轴于点M，交x轴于点H．则 
= 
，
∴OM=OE=5，
∴点M坐标（0，﹣5）．
设直线ME的解析式为y=k1x﹣5，
∴3k1﹣5=﹣4，
∴k1= 
，
∴直线ME解析式为y= x﹣5，
令y=0，得 x﹣5=0，解得x=15，
∴点H坐标（15，0），
∵MH∥PB，
∴ 
= 
，即 
= 
，
∴m=﹣ 
，
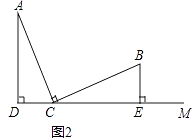
②如图2，
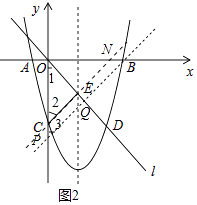
当QO=QP时，△POQ是等腰三角形．
∵当x=0时，y= x2﹣3x﹣8=﹣8，
∴点C坐标（0，﹣8），
∴CE= 
=5，
∴OE=CE，
∴∠1=∠2，
∵QO=QP，
∴∠1=∠3，
∴∠2=∠3，
∴CE∥PB，
设直线CE交x轴于N，解析式为y=k2x﹣8，
∴3k2﹣8=﹣4，
∴k2= ，
∴直线CE解析式为y= x﹣8，
令y=0，得 x﹣8=0，
∴x=6，
∴点N坐标（6，0），
∵CN∥PB，
∴ 
= 
，
∴ 
= 
，
∴m=﹣ 
．
③OP=PQ时，显然不可能，理由，
∵D（6，﹣8），
∴∠1＜∠BOD，
∵∠OQP=∠BOQ+∠ABP，
∴∠PQO＞∠1，
∴OP≠PQ，
综上所述，当m=﹣ 或﹣ 时，△OPQ是等腰三角形
【解析】（1）待定系数法求解可得；（2）求得直线l的解析式和抛物线对称轴即可得出交点坐标；（3）根据△FOB和△EOB共底且面积相等可得yF=yE ， 即 x2﹣3x﹣8=﹣4，解之可得答案；（4）①如图1中，当OP=OQ时，△OPQ是等腰三角形，过点E作直线ME∥PB，交y轴于点M，交x轴于点H，求出点M、H的坐标即可解决问题．②如图2中，当QO=QP时，△POQ是等腰三角形，先证明CE∥PQ，根据平行线的性质列出方程即可解决问题．
