Question

【题目】某一空间图形的三视图如下图所示，其中主视图：半径为1的半圆以及高为1的矩形；左视图：半径为1的四分之一圆以及高为1的矩形；俯视图：半径为1的圆，求此图形的体积．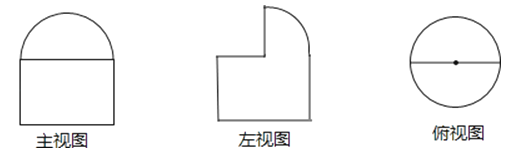

Answer 1

【答案】解：由已知可得该几何体是一个下部为半圆柱，上部为球的组合体
由三视图可得，下部圆柱的底面半径为1，高为1，则V圆柱=π
上部球的半径为1，则球=π
故此几何体的体积为．
【解析】由已知中的三视图，我们可以判断出该几何体的形状为：下部是底面半径为1，高为1的圆柱，上部为半径为1的球，组成的组成体，代入圆柱体积公式和球的体积公式，即可得到答案．
【考点精析】本题主要考查了由三视图判断几何体的相关知识点，需要掌握在三视图中，通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数；通过主视图、左视图可以确定行与列中的最高层数才能正确解答此题．