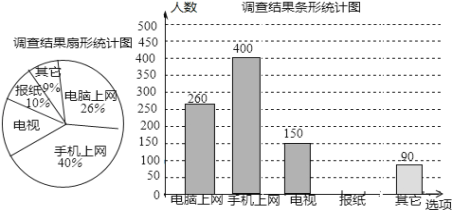
题目内容
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1, 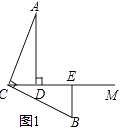
①线段CD和BE的数量关系是;
②请写出线段AD,BE,DE之间的数量关系 .
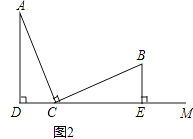
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系. 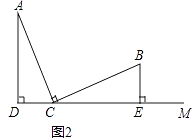
【答案】
(1)CD=BE;AD=BE+DE
(2)解:②中的结论不成立.结论:DE=AD+BE.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,
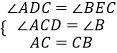 ,
,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∵DE=CD+CE=BE+AD,
∴DE=AD+BE.
【解析】解:(1)①结论:CD=BE. 理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,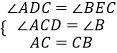 ,
,
∴△ACD≌△CBE,
∴CD=BE.
②结论:AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.

练习册系列答案
相关题目
【题目】我国有五座名山,但在洪雅人的心目中,我国有六座名山,这六座名山的海拔分别为:
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔(米) | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
(1)海拔最高的山是多少,最高的山与最低的山的海拔相差多少米;
(2)海拔不低于1500米的山的频数是多少;频率是多少;
(3)根据数据制作条形统计图.