题目内容
【题目】已知:在△ABC中, ∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
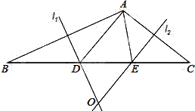
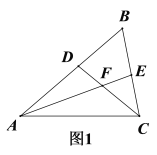
(1)如图1,若AE、CD为△ABC的角平分线. ①求证: ∠AFC=120°;②若AD=6,CE=4,求AC的长?
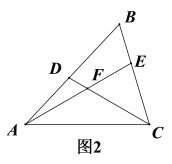
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
【答案】(1)①见解析;②AC=10;(2)见解析
【解析】
(1)①根据角平分线的定义、三角形内角和定理计算;
②在AC上截取AG=AD=6,连接FG,证明△ADF≌△AGF、△CGF≌△CEF,根据全等三角形的性质解答;
(2)在AE上截取FH=FD,连接CH,证明△ADF≌△CHF,根据全等三角形的性质、三角形的外角的性质解答.
(1)①∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠BCA,
∠BCA,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180°-∠FAC-∠FCA=180°-![]() (∠BAC+∠BCA)=120°;
(∠BAC+∠BCA)=120°;
②在AC上截取AG=AD=6,连接FG,
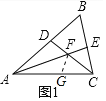
∵AE、CD分别为△ABC的角平分线,
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中,
∵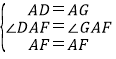
∴△ADF≌△AGF(SAS),
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中,
∵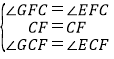
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10;
(2)在AE上截取FH=FD,连接CH,
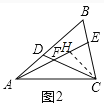
∵∠FAC=∠FCA=30°,
∴FA=FC,
在△ADF和△CHF中,
∵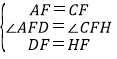 ,
,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF,
∠CHE=∠HAC+∠HCA=60°+∠HCF,
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我国有五座名山,但在洪雅人的心目中,我国有六座名山,这六座名山的海拔分别为:
山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨嵋山 | 瓦屋山 |
海拔(米) | 1152 | 1997 | 1873 | 1500 | 1309 | 2830 |
(1)海拔最高的山是多少,最高的山与最低的山的海拔相差多少米;
(2)海拔不低于1500米的山的频数是多少;频率是多少;
(3)根据数据制作条形统计图.