题目内容
【题目】如图,直线![]() 与x轴交于点M,与y轴交于点A,过点A作
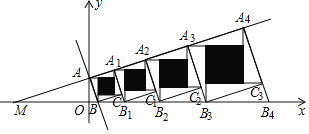
与x轴交于点M,与y轴交于点A,过点A作![]() ,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,
,交x轴于点B,以AB为边在AB的右侧作正方形ABCA1,延长A1C交x轴于点B1,以A1B1为边在A1B1的右侧作正方形A1B1C1A2…按照此规律继续作下去,再将每个正方形分割成四个全等的直角三角形和一个小正方形,每个小正方形的每条边都与其中的一条坐标轴平行,正方形ABCA1,A1B1C1A2,…,![]() 中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
中的阴影部分的面积分别为S1,S2,…,Sn,则Sn可表示为_____.
【答案】![]() .
.
【解析】
因为所有的正方形都相似,所以只要求出第一个阴影正方形的面积和第二个阴影正方形与第一个阴影正方形的相似比即可依此规律求解.根据题意和正方形的性质可得![]() ,所以它们的正切相等,等于
,所以它们的正切相等,等于![]() ,据此可求出OB的长,再用OA-OB即为第一个阴影正方形的边长,于是S1可得;同理可求得
,据此可求出OB的长,再用OA-OB即为第一个阴影正方形的边长,于是S1可得;同理可求得![]() 与AB的关系,进而可求得
与AB的关系,进而可求得![]() 与
与![]() 的关系;以此规律类推可求得Sn与S1的关系,整理即得答案.
的关系;以此规律类推可求得Sn与S1的关系,整理即得答案.
解:在直线![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵正方形ABCA1中的四个小正方形都与△AOB全等,
∴第一个阴影正方形的边长为:![]() ,
,
∴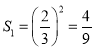 ,
,
同理:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得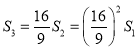 ,
, ,…,
,…,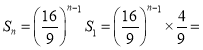
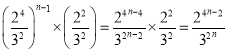 .
.
故答案为:![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目