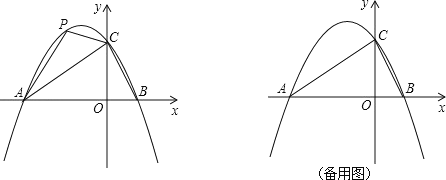Question

【题目】如图,二次函数y=x2+bx+c的图象与x轴交于A.B两点,且A点坐标为(3,0),经过B点的直线y=x-1交抛物线于点D.

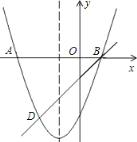
(1)求B点坐标和抛物线的解析式

(2)点D的坐标

(3)过x轴上点E(a,0)(E点在B点的右侧)作直线EF∥BD，交抛物线于点F，是否存在实数a使四边形BDFE是平行四边形?如果存在，求出满足条件的a；如果不存在，请说明理由.

Answer 1

【答案】(1) y=x2+2x3，(1,0)；(2)点D坐标（-2，-3）；(3)存在实数a=3，使四边形BDFE是平行四边形

【解析】

（1）设抛物线为y=x2+bx+c，求出B点的坐标，把点A(3,0),B(1,0)代入解析式中求出 b，c的值即可求出抛物线的解析式；

（2）求出抛物线与直线y=x-1的交点，然后把x=-2代入直线y=x-1即可求出D的坐标；

（3）得到用a表示的EF的解析式，跟二次函数解析式组成方程组，得到含y的一元二次方程，进而根据y=-3求得合适的a的值即可．

(1) B点在直线y=x-1上

令y=0，则x=1

∴B的坐标为(1,0)

由题意知将A(3,0),B(1,0)的坐标代入y=x2+bx+c得，

，

解得： ，

∴y=x2+2x3

(2)由（1）知y=x2+2x3，

得：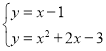

解得：

∴D坐标（-2，y）

∵直线B的解析式为y=x-1,

解得：y=-3

∴点D坐标（-2，-3）

(3)如图：

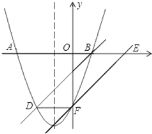
∵直线B的解析式是y=x1,且EF∥BD，

∴直线EF的解析式为：y=xa，

若四边形BDFE是平行四边形，

则DF∥x轴，

∴D、F两点的纵坐标相等，即点F的纵坐标为3.

由 ，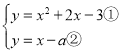

由②得,x=y+a,代入方程①得，

y2+(2a+1)y+a2+2a3=0，

解得：

令=-3

解得：a1=1，a2=3.

当a=1时,E点的坐标(1,0)，这与B点重合，舍去；

∴当a=3时,E点的坐标(3,0)，符合题意。

∴存在实数a=3，使四边形BDFE是平行四边形.