Question

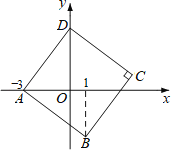
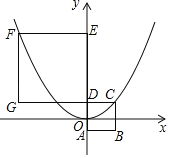
【题目】如图，四边形ABCD、DEFG都是正方形，边长分别为m、n（m＜n）．坐标原点O为AD的中点，A、D、E在y轴上．若二次函数y＝ax2的图象过C、F两点，则＝_____．

Answer 1

【答案】

【解析】

由正方形ABCD的边长为m，坐标原点O为AD的中点，得出C（m，m）．将C点坐标代入y=ax2，求出a=，则抛物线解析式为y=x2，再将F（-n，n+m）代入y=x2，整理得出方程m2-2mn-n2=0，把m看作常数，利用求根公式得出n=（1±）m（负值舍去），那么.

解：∵正方形ABCD的边长为m，坐标原点O为AD的中点，

∴C（m，m）．

∵抛物线y＝ax2过C点，

∴m＝am2，解得a＝，

∴抛物线解析式为y＝x2，

将F（﹣n，n）代入y＝x2，

得n＝×（﹣n）2，

整理得m2﹣2mn﹣n2＝0，

解得n＝（1±）m（负值舍去），

∴＝1+.

故答案为1+．