题目内容
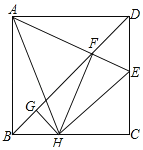
【题目】如图,四边形ABCD为菱形,以AD为直径作![]() 交AB于点F,连接DB交
交AB于点F,连接DB交![]() 于点H,E是BC上的一点,且
于点H,E是BC上的一点,且![]() ,连接DE.
,连接DE.

(1)求证:DE是![]() 的切线.
的切线.
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)![]() 的半径为
的半径为![]() .
.
【解析】
(1)如图1,连接DF,先根据菱形的性质和SAS证明△DAF≌△DCE,得![]() ,再由AD是圆的直径得∠AFD=90°,于是∠DEC=90°,然后利用
,再由AD是圆的直径得∠AFD=90°,于是∠DEC=90°,然后利用![]() 可得∠ADE=90°,问题即得证明;
可得∠ADE=90°,问题即得证明;
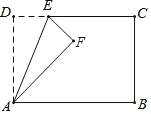
(2)如图2,连接AH,先根据等腰三角形三线合一的性质得出![]() ,再由DF是
,再由DF是![]() 和
和![]() 的公共的直角边,根据勾股定理列出关于AD的方程,解方程即可求出AD的长,进一步即可求出圆的半径.
的公共的直角边,根据勾股定理列出关于AD的方程,解方程即可求出AD的长,进一步即可求出圆的半径.
(1)证明:如图1,连接DF,
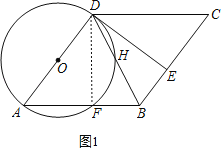
∵四边形ABCD为菱形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() .
.
∵AD是![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵OD是![]() 的半径,∴DE是
的半径,∴DE是![]() 的切线;
的切线;
(2)解:如图2,连接AH,
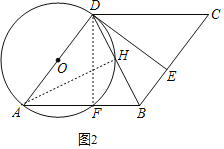
∵AD是![]() 的直径,∴
的直径,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的半径为
的半径为![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目