题目内容
【题目】阅读下列材料，回答问题：
如图，
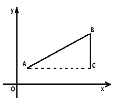
点A（x1，y1），点B（x2，y2），以AB为斜边作Rt△ABC，则C（x2，y1），于是
，
，所以
，反之，可将代数式
的值看作点（x1，y1）到点（x2，y2）的距离.
例如：
故代数式的值看作点（x，y）到点（1，-1）的距离.
已知：代数式
（1）该代数式的值可看作点（x，y）到点 、 的距离之和.
（2）求出这个代数式的最小值,
（3）在（2）的条件下求出此时y与x之间的函数关系式并写出x的值范围.
【答案】（1）（1，－8）, （－2，2）; （2）
;（3）
【解析】
（1）利用配方法将代数式中的被开方数配成完全平方式，再根据题中给出的两点之间距离的定义即可求出结果.
（2）画出图形观察即可发现当点（x，y）与点（1，－8），（－2，2）在同一条直线上，并且点（x，y）位于点（1，－8），（－2，2）的之间时，代数式的值最小；
（3）利用待定系数法，列出二元一次方程组解出未知数的值即可.
解：（1）根据材料知：
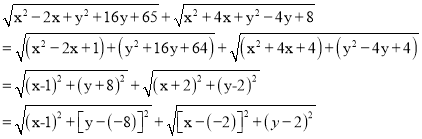
所以可将代数式
的值看作点（x，y）到点（1，－8）的距离与点（x，y）到点（－2，2）的距离之和.
（2）当代数式取最小值时,即点（x，y）与点（1，－8），（－2，2）在同一条直线上，并且点（x，y）位于点（1，－8），（－2，2）的中间，
∴的最小值
（3）设过（x，y），且－2≤x≤1,（1，－8），（－2，2）的直线解析式为：y=kx+b则
解得：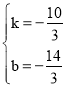
∴
练习册系列答案
相关题目
