��Ŀ����
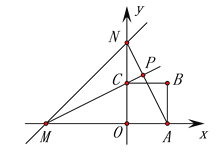
����Ŀ����ͼ�Ƕ��κ���y��ax2��bx��c��a��0���IJ���ͼ�����е�A��-1,0����x���ϵ�һ�����㣬��C��y���ϵĽ��㣮
��1��������A��ֱ��l��������κ�����ͼ�����һ������ΪD�����ͼ��ĶԳ��ύ�ڵ�E����y�ύ�ڵ�F����DE��EF��FA��
����![]() ��ֵ��
��ֵ��
����������κ���ͼ��Ķ���ΪP���ʣ���DFΪֱ����Բ�ܷ���P�����ܣ��������ʱ���κ����Ĺ�ϵʽ�������ܣ���˵�����ɣ�
��2������C����Ϊ��0��-1������S��a��b��c ����S��ȡֵ��Χ��

���𰸡�(1)��![]() ����
����![]() ����2)
����2) ![]()
�������������������1������A��-1��0�����õ�OA=1����DE=EF=FA���õ�AO=OM=MN�� OC=ND����OF��ND���õ�![]() ���Ӷ��õ�������
���Ӷ��õ�������
����OA=1��AO=OM=MN���õ�OM=MN=1���Գ���Ϊx=1���Ӷ��õ�b=-2a����������x�����һ������Ϊ��3��0�����õ�0=9a-6a+c���õ�c=-3a����y=ax2-2ax-3a���õ�OC=ND=3a�� OF=a���õ�D��F��E��P�������������õ�PE=2a��FE=ED=![]() ��
��
����DFΪֱ����Բ�ܷ���Pʱ��PE=FE=ED����2a=![]() ���ⷽ�̼��ɵõ�������
���ⷽ�̼��ɵõ�������
��2���ɶ��κ���y��ax2��bx��c��a��0����A��-1��0����C��0��-1�����õ�c=-1��b=a-1�� ��S=2a-2����a��0�����ɵõ�������
���������������1���١�A��-1��0������OA=1����DE=EF=FA����AO=OM=MN����OC=ND����OF��ND���� ![]() ����
����![]() ��
��

�ڡ�OA=1��AO=OM=MN����OM=MN=1����Գ���Ϊx=1���� ![]() ����b=-2a����������x�����һ������Ϊ��3��0������0=9a-6a+c�������c=-3a����y=ax2-2ax-3a����OC=ND=3a����OF=a����D��2��-3a����F��0��-a����E(1��-2a)��P��1��-4a������PE=2a��
����b=-2a����������x�����һ������Ϊ��3��0������0=9a-6a+c�������c=-3a����y=ax2-2ax-3a����OC=ND=3a����OF=a����D��2��-3a����F��0��-a����E(1��-2a)��P��1��-4a������PE=2a��![]() ��
��
����DFΪֱ����Բ�ܷ���Pʱ��PE=FE=ED����2a=![]() �������
������� ![]() ��������ȥ������
��������ȥ������![]() ����
����![]() ��
��
��2���������y��ax2��bx��c��a��0����A��-1��0����C��0��-1������a-b+c=0��c=-1����b=a-1����S=a+b+c=a+a-1-1=2a-2����a��0����S=2a-2����2��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij����С���A�س������ڶ��������·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ��¼����.����λ��![]() ��
��
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� |
|
|
|
|
|
|
|
��1�����չ�ʱ������С����![]() �صĺη�����
�صĺη�����![]() �ض�Զ��
�ض�Զ��
��2���ڵڼ��μ�¼ʱ��![]() ����Զ��
����Զ��
��3����������ʻÿǧ����0.4�����ʴ�![]() �س��������������ٻص�
�س��������������ٻص�![]() �ع����Ͷ�������
�ع����Ͷ�������
����Ŀ�����������ҹ��ܶ����������������������ij����Ϊ�˵��鱾�������������������Ҫ�������ʶ���������Ը��������־���������ʾ����飬Ҫ�����������Ҫ������ֻѡ�����е�һ����������Ҫ����д���ʾ��������Ե��������������������������²�������ͳ��ͼ�������������ѡ���ѡ������ͳ�Ʊ�
������������Ҫ���� | Ƶ���������� |
A������ѹ�ͣ����������� | m |
B����ҳ�����ʪ�ȵ� | 40 |
C����β���ŷ� | n |
D������ɵ���Ⱦ | 120 |
E���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺

��1����գ�m=________��n=________������ͳ��ͼ��Cѡ����ռ�İٷֱ�Ϊ________��
��2��������������Լ��6 000�ˣ���������л�ѡ��Dѡ��ľ���������
��3������������������������⣬�����ü�̵����Է������飮