题目内容
【题目】感知:如图(1),已知正方形ABCD和等腰直角△EBF,点E在正方形BC边上,点F在AB边的延长线上,∠EBF=90°,连结AE、CF.
易证:∠AEB=∠CFB(不需要证明).
探究:如图(2),已知正方形ABCD和等腰直角△EBF,点E在正方形ABCD内部,点F在正方形ABCD外部,∠EBF=90°,连结AE、CF.
求证:∠AEB=∠CFB
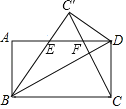
应用:如图(3),在(2)的条件下,当A、E、F三点共线时,连结CE,若AE=1,EF=2,则CE=______.

【答案】感知:见解析;探究:见解析;应用:![]() .
.
【解析】
感知:先判断出∠ABC=∠CBF=90°,AB=BC,进而判断出BE=BF,得出△ABE≌△CBF(SAS)即可得出结论;
探究:先判断出∠ABE=∠CBF,进而得出△ABE≌△CBF(SAS),即可得出结论;
应用:先求出CF=1,再判断出∠CFE=90°,利用勾股定理即可得出结论.
解:感知:∵四边形ABCD是正方形,
∴∠ABC=∠CBF=90°,AB=BC,
∵△BEF是等腰直角三角形,
∴BE=BF,
∴△ABE≌△CBF(SAS),
∴∠AEB=∠CFB;
探究:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△BEF是等腰直角三角形,
∴BE=BF,∠EBF=90°=∠ABC,
∴∠ABE=∠CBF,
∴△ABE≌△CBF(SAS),
∴∠AEB=∠CFB;
应用:由(2)知,△ABE≌△CBF,∠BFC=∠BEA,
∴CF=AE=1,
∵△BEF是等腰直角三角形,
∴∠BFE=∠BEF=45°,
∴∠AEB=135°,
∴∠BFC=135°,
∴∠CFE=∠BFC-∠BFE=90°,
在Rt△CFE中,CF=1,EF=2,根据勾股定理得, ![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目