题目内容
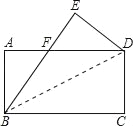
【题目】如图,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F.
(1)若AB=4,BC=8,求DF的长;
(2)当DA平分∠EDB时,求![]() 的值.
的值.
【答案】(1)DF=5;(2)![]() .
.
【解析】
(1)易证BF=FD,在直角△ABF中,根据勾股定理就可以求出DF的长;(2)已知DA平分∠EDB,根据矩形的角是直角,就可以求出∠ADB,∠BDC的度数,就可以把求两线段的比值的问题转化为三角函数的问题.
(1)∵AD∥BC,
∴∠DBC=∠FDB,
又∵∠DBC=∠DBE,
∴∠FDB=∠FBD,
∴BF=FD,
设AF=x,则BF=DF=8﹣x,
在Rt△ABF中,根据勾股定理得到42+x2=(8﹣x)2,
解得x=3,
∴DF=8﹣3=5;
(2)∵DA平分∠EDB,
即∠EDA=∠ADB,
设∠EDA=∠ADB=y°,则∠EDB=2y°,
∴∠BDC=2y°,
∵∠ADC=90°,
∴3y=90°,
解得y=30°,
∴∠DBC=30°,
在Rt△CDB中,tan∠DBC=![]() =tan30°=
=tan30°=![]() ,
,
又∵AB=CD,
∴![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=﹣1,y=1 | x=1,y=0 | x=3,y=2 | x=1,y=1 | x=5,y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请结合上述的有关信息,计算4×3.142﹣4×3.14×3.28+3.282.