题目内容
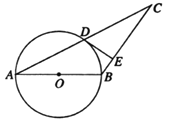
【题目】如图,己知等腰![]() ,以
,以![]() 为直径的圆交
为直径的圆交![]() 于点
于点![]() ,过点
,过点![]() 的⊙
的⊙![]() 的切线交
的切线交![]() 于点
于点![]() ,若
,若![]() ,则⊙
,则⊙![]() 的半径是( )
的半径是( )
A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
【答案】B
【解析】
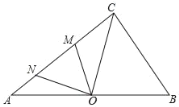
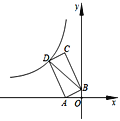
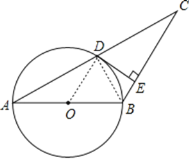
首先连接OD、BD,判断出OD∥BC,再根据DE是⊙O的切线,推得DE⊥OD,所以DE⊥BC;然后根据DE⊥BC,CD=4![]() ,CE=8,求出DE的长度是多少;最后判断出BD、AC的关系,根据勾股定理,求出BC的值是多少,再根据AB=BC,求出AB的值是多少,即可求出⊙O的半径是多少.
,CE=8,求出DE的长度是多少;最后判断出BD、AC的关系,根据勾股定理,求出BC的值是多少,再根据AB=BC,求出AB的值是多少,即可求出⊙O的半径是多少.
如图,连接OD、BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
又∵AB=BC,
∴AD=CD,
又∵AO=OB,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE是⊙O的切线,
∴DE⊥OD,
∴DE⊥BC,
∵CD=4![]() ,CE=8,
,CE=8,
∴DE=![]() =4,
=4,
∵S△BCD=BDCD÷2=BCDE÷2,
∴4![]() BD=4BC,即
BD=4BC,即![]() BD=BC,
BD=BC,
∴BD=![]() BC,
BC,
∵BD2+CD2=BC2,
∴(![]() BC)2+(4
BC)2+(4![]() )=BC2,
)=BC2,
解得BC=10,
∵AB=BC,
∴AB=10,
∴⊙O的半径是;10÷2=5.
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目