题目内容
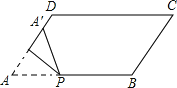
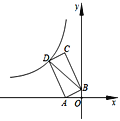
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
【答案】-16
【解析】
过D作DM⊥x轴于M,根据相似三角形的性质和判定求出DM=2AM,根据三角形的面积求出x,即可求出DM和OM,得出答案即可.
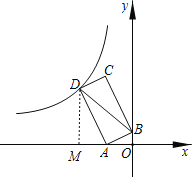
∵点A(-2,0),B(0,1),
∴OA=2,OB=1,
过D作DM⊥x轴于M,则∠DMA=90°,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DMA=∠DAB=∠AOB=90°,
∴∠DAM+∠BAO=90°,∠DAM+∠ADM=90°,
∴∠ADM=∠BAO,
∴△DMA∽△AOB,
∴![]() =2,
=2,
即DM=2MA,
设AM=x,则DM=2x,
∵四边形OADB的面积为6,
∴S梯形DMOB-S△DMA=6,
∴![]() (1+2x)(x+2)-
(1+2x)(x+2)-![]() 2xx=6,
2xx=6,
解得:x=2,
则AM=2,OM=4,DM=4,
即D点的坐标为(-4,4),
∴k=-4×4= -16,

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目