题目内容
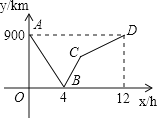
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇0.5小时后,第二列快车与慢车相遇.则第二列快车比第一列快车晚出发__小时.
【答案】![]() .
.
【解析】
假设快车的速度为a(km/h),慢车的速度为b(km/h).当两车相遇时,两车各自所走的路程之和就是甲乙两地的距离,由此列式4a+4b=900①,另外,由于快车到达乙地的时间比慢车到达甲地的时间要短,图中的(12,900)这个点表示慢车刚到达甲地,这时的两车距离等于两地距离,而x=12就是慢车正好到达甲地的时间,所以,12b=900,①和②可以求出,快车速度a=150(km/h),慢车速度b=75(km/h);其中C点代表快车到站,而900÷150=6,6×75=450,所以C点(6,450),然后利用待定系数法可以确定BC段的函数解析式为y=225x-900(4≤x≤6),最后设第二列快车出发后x小时与慢车相遇,根据已知条件列出方程4.5×75+150x=900,解方程即可求解.
设快车的速度为a(km/h),慢车的速度为b(km/h),
∴4(a+b)=900,
∵慢车到达甲地的时间为12小时,
∴12b=900,
b=75,
∴4(a+75)=900,
a=150;
∴快车的速度为150km/h,慢车的速度为75km/h;
又C点代表快车到站,而900÷150=6,6×75=450,
所以C点(6,450),
设BC段解析式为y=kx+b,
再把B(4,0),C(6,450)代入求得k=225,b=-900.
即y=225x-900(4≤x≤6),
设第二列快车出发后x小时与慢车相遇,
得4.5×75+150x=900,
解得x=![]() ,
,
4+0.5-![]() =
=![]() 小时.
小时.
∴第二列快车比第一列快车晚出发![]() 小时.
小时.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案