题目内容
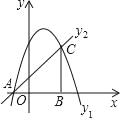
【题目】如图,动点A在抛物线y=-x2+2x+3(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A作AC⊥l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是( )

A.2≤BD≤3B.3≤BD≤6C.1≤BD≤6D.2≤BD≤6
【答案】D
【解析】
根据题意先利用配方法得到抛物线的顶点坐标为(1,4),再根据矩形的性质得BD=AC,由于2≤AC≤6,从而进行分析得到BD的取值范围.
解:∵![]() ,
,
∴抛物线开口向下,顶点坐标为(1,4),
∵四边形ABCD为矩形,
∴BD=AC,
∵直线l经过点(0,6),且与y轴垂直,抛物线y=-x2+2x+3(0≤x≤3),
∴2≤AC≤6,
∴另一对角线BD的取值范围为:2≤BD≤6.
故选:D.

练习册系列答案
相关题目