题目内容
如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)在抛物线的对称轴上找一点M,使得MD+MC的值最小,并求出点M的坐标;
(3)设点C关于抛物线对称的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)A(4,0) 、D(-2,0)、C(0,-3);(2)连接AC,则AC与抛物线的对称轴交点M即为所求,M (1, );(3)存在,(-2,0)或(6,6).
);(3)存在,(-2,0)或(6,6).
解析试题分析:(1)在 中令
中令 ,解得
,解得 ,
,
∴A(4,0) 、D(-2,0).
在 中令
中令 ,得
,得 ,∴C(0,-3).
,∴C(0,-3).
(2)连接AC,根据轴对称的性质,AC与抛物线的对称轴交点M即为所求,从而应用待定系数法求出AC的解析式,再求出抛物线的对称轴,即可求得点M的坐标.
(3)分BC为梯形的底边和BC为梯形的腰两种情况讨论即可.
试题解析:(1)A(4,0) 、D(-2,0)、C(0,-3)
(2)如图,连接AC,则AC与抛物线的对称轴交点M即为所求.
设直线AC的解析式为 ,则
,则 ,解得
,解得 .
.
∴直线AC的解析式为 .
.
∵ 的对称轴是直线
的对称轴是直线 ,
,
把x=1代入 得
得
`∴M(1, ).
).
(3)存在,分两种情况:
①如图,当BC为梯形的底边时,点P与D重合时,四边形ADCB是梯形,此时点P为(-2,0).
②如图,当BC为梯形的腰时,过点C作CP//AB,与抛物线交于点P,
∵点C,B关于抛物线对称,∴B(2,-3)
设直线AB的解析式为 ,则
,则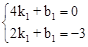 ,解得
,解得 .
.
∴直线AB的解析式为 .
.
∵CP//AB,∴可设直线CP的解析式为 .
.
∵点C在直线CP上,∴ .
.
∴直线CP的解析式为 .
.
联立 ,解得
,解得 ,
,
∴P(6,6).
综上所述,在抛物线上存在点P,使得以A、B、C、P四点为顶点的四边形为梯形,点P的坐标为(-2,0)或(6,6).
考点:1.二次函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.轴对称的应用(最短线路问题);5.二次函数的性质;6.梯形存在性问题;7.分类思想的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.
x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.
 (
( 为常数,且
为常数,且 )与
)与 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线 与抛物线的另一交点为D.
与抛物线的另一交点为D.
 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
 x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
 .
.