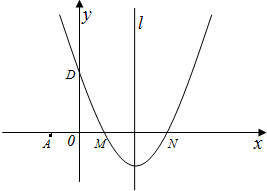Question

平面直角坐标系中，抛物线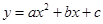交轴于A、B两点（点A在点B左侧），与轴交于点C，点A、C的坐标分别为（-3,0），（0,3），对称轴直线交轴于点E,点D为顶点.
（1）求抛物线的解析式；
（2）点P是直线AC下方的抛物线上一点，且,，求点P的坐标；
（3）点M是第一象限内抛物线上一点，且∠MAC=∠ADE，求点M的坐标.

Answer 1

（1）y=-x²-2x+3；（2）（-4，-5）或（1，0）；（3）（，）．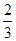

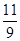解析试题分析：（1）由已知中点A、C的坐标分别为（-3，0），（0，3），对称轴为直线x=-1，得出B点坐标，进而利用交点式求出即可求出抛物线的解析式；
（2）由已知中C点坐标，再假设出P点坐标，可求出直线PC解析式，求出R点坐标，进而根据S_△PAC=2S_△DAC，可得点P的坐标；
（3）过点C作CH⊥DE交DE于点H，设AC交对称轴于点G，AM交y轴于点N，由∠MAC=∠ADE，可得N点坐标，进而求出CN的方程，联立直线与抛物线方程可得M点坐标．
（1）由对称轴x=-1，A（-3，0），可得B点坐标（1，0）
设y=a（x+3）（x-1），把C（0，3）代入得，4=-8a，
解得：a=-1，
所求解析式为：y=-x²-2x+3；
（2）如图：y=-x²-2x+3=-（x+1）²+4，顶点D（-1，4），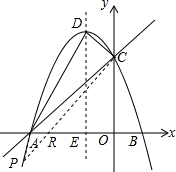

由A（-3，0）、C（0，3），得直线AC解析式为y=x+3；
设对称轴交AC于点G，则G（-1，2），∴S_△DAC=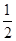（4-2）×3=3，
设P点（m，-m²-2m+3），
设PC解析式为：y=qx+p，
∴，
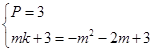解得：k=-m-2，
∴PC解析式为：y=（-m-2）x+3，
设PC与x轴交于点R，
∴R（，0），
∴AR=3+，
∴S_△APR+S_△CAR=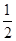（3+）×（m²+2m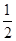-3）+×（3+）×3=+，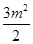
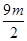则S_△PAC=+，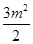
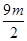由S_△PAC=2S_△DAC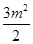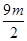，∴+=2×3，
解得：m₁=-4，m₂=1，
把m₁=-4，m₂=1分别代入y=-x²-2x+3中，
∴y₁=-5，y₂=0，
∴P点坐标为（-4，-5）或（1，0）；
（3）由以上可得出：D（-1，4），C（0，3），E（-1，0），
如备用图：过点C作CH⊥DE交DE于点H，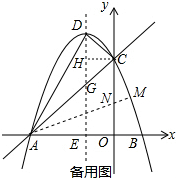

∴H（-1，3），CH=DH=1，∠DCH=∠HCA=∠CA0=45°，
∴CD=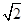，AC=3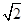，△ACD为直角三角形，且tan∠DAC=．
设AC交对称轴于点G，AM交y轴于点N，
∵∠DAC+∠ADE=∠DGC=45°，∠CAM+∠MAO=∠CAO=45°，∠ADE=∠CAM，∠DAC=∠MAO，
∴tan∠MAO=．
∵A（-3，0），
∴ON=1，即N（0，1），
设直线CN解析式为：y=dx+h
∴，
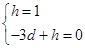解得：，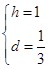
∴直线CN解析式为y=x+1，
联立方程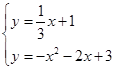
得：x=-3（舍）或x=，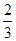
∴点M的坐标为（，）．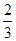
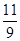考点：二次函数综合题．