题目内容
【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍．
即：如图1，.
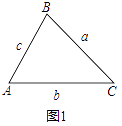
在△ABC中，已知AB=c，BC=a，CA=b，则有：
a2=b2+c2﹣2bccosA，b2=a2+c2﹣2accosB，c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题：
例在△ABC中，已知a=2 
，b=2 
，c= 
，求∠A．
解：∵a2=b2+c2﹣2bccosA，
cosA= 
= 
= 
．
∴∠A=60°．
【应用新知】
（1）选择题：在△ABC中，已知b=ccosA，a=csinB，那么△ABC是（ ）．
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
（2）如图2，
某客轮在A处看港口D在客轮的北偏东50°，A处看灯塔B在客轮的北偏西30°，距离为2 海里，客轮由A处向正北方向航行到C处时，再看港口D在客轮的南偏东80°，距离为6海里．求此时C处到灯塔B的距离．
【答案】
（1）C
（2）
∠ADC=180°﹣80°﹣50°=50°，
∴CA=CD=6，
BC2=AB2+AC2﹣2ABACcos∠BAC=（2 
）2+62﹣2×3 
×6× 
=12，
∴BC=2 ，
答：C处到灯塔B的距离为2 海里
【解析】解：（1）∵b=ccosA，a=csinB，
∴cosA= 
，sinB= 
，
∴a2=b2+c2﹣2bccosA=b2+c2﹣2bc× 
=b2﹣c2 ，
∴a2+c2=b2 ，
∴△ABC是直角三角形，∠B=90°，
∴a=csinB=c，
∴△ABC是等腰直角三角形，
故选：C．
【考点精析】关于本题考查的关于方向角问题，需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能得出正确答案．
练习册系列答案
相关题目
