题目内容
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线
与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线![]() .
.
(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线![]() 的对称点为N,试证明四边形CDAN是平行四边形;
的对称点为N,试证明四边形CDAN是平行四边形;
(3)点P在直线![]() 上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.

【答案】(1)∴y=﹣x2+2x+3,对称轴为直线x=1,顶点M(1,4);(2)证明见解析; (3)P1(1,﹣4+2![]() ),P2(1,﹣4﹣2
),P2(1,﹣4﹣2![]() ).
).
【解析】试题分析:(1)将A、C两点坐标代入解析式即可求出![]() ,将解析式配成顶点式即可得到对称轴方程和顶点坐标;
,将解析式配成顶点式即可得到对称轴方程和顶点坐标;
(2)先由C、M两点坐标求出直线CM解析式,进而求出D点坐标,由于C、N两点关于抛物线对称轴对称,则CN∥AD,同时可求出N点坐标,然后得出CN=AD,结论显然;
(3)设出P点纵坐标,表示出MP的长度,过点P作![]() 于H,表示出PH的长度,在Rt△APE中中用勾股定理列出方程,解之即得答案.
于H,表示出PH的长度,在Rt△APE中中用勾股定理列出方程,解之即得答案.
试题解析:(1)∵抛物线![]() 经过点A(1,0)和点C(0,3),
经过点A(1,0)和点C(0,3),
![]()
![]()
![]()
对称轴为直线x=1,顶点M(1,4);
(2)如图1,
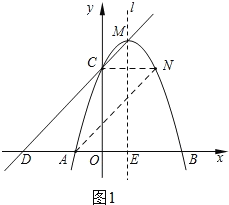
∵点C关于直线l的对称点为N,
∴N(2,3),
∵直线y=kx+b经过C.M两点,
∴![]()
∴![]()
∴y=x+3,
∵y=x+3与x轴交于点D,
∴D(3,0),
∴AD=2=CN
又∵AD![]() CN,
CN,
∴CDAN是平行四边形;
(3)设P(1,a),过点P作PH⊥DM于H,连接PA、PB,如图2,
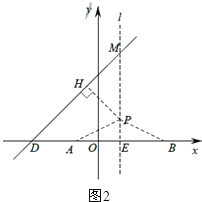
则MP=4a,
又![]()
![]()
Rt△APE中, ![]()
![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目