Question

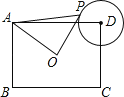
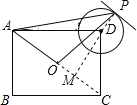
【题目】如图，在矩形ABCD中，AB＝3，BC＝4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP，OP，则△AOP面积的最大值为_____．

Answer 1

【答案】

【解析】

当P点移动到平行于OA且与⊙D相切时，△AOP面积的最大，由于P为切点，得出MP垂直与切线，进而得出PM⊥AC，根据勾股定理先求得AC的长，进而求得OA的长，根据△ADM∽△ACD，求得DM的长，从而求得PM的长，最后根据三角形的面积公式即可求得；

解：当P点移动到过点P的直线平行于OA且与⊙D相切时，△AOP面积的最大，如图，

∵过P的直线是⊙D的切线，

∴DP垂直于切线，

延长PD交AC于M，则DM⊥AC，

∵在矩形ABCD中，AB＝3，BC＝4，

∴AC＝，

∴OA＝，

∵∠AMD＝∠ADC＝90°，∠DAM＝∠CAD，

∴△ADM∽△ACD，

∴，

∵AD＝4，CD＝3，AC＝5，

∴DM＝ ，

∴PM＝PD+DM＝1+＝ ，

∴△AOP的最大面积＝OAPM＝××＝，

故答案为：．