题目内容
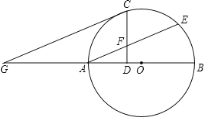
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连结OC,由C是劣弧AE的中点,根据垂径定理得OC⊥AE,而CG∥AE,所以CG⊥OC,然后根据切线的判定定理即可得到结论;
(2)连结AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF;
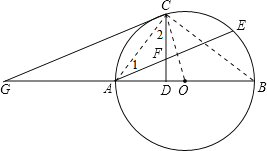
解:(1)证明:连结OC,如图,
∵C是劣弧AE的中点,∴OC⊥AE,
∵CG∥AE,∴CG⊥OC,
∴CG是⊙O的切线;
(2)证明:连结AC、BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠2+∠BCD=90°,
而CD⊥AB,∴∠B+∠BCD=90°,
∴∠B=∠2,
∵AC弧=CE弧,
∴∠1=∠B,
∴∠1=∠2,
∴AF=CF;(也可由OA=OC直接证)

练习册系列答案
相关题目