题目内容
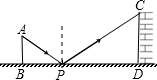
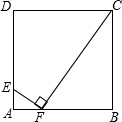
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6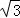 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6
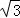 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
(1)证明见解析;(2)6.
试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在在Rt△ADE中,利用勾股定理求出线段AE的长度.
(1)证明:∵?ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
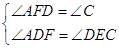
∴△ADF∽△DEC.
(2)∵△ADF∽△DEC,
∴
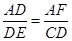
又 ∵ CD=AB=8,AD=6
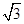 ,AF= 4
,AF= 4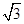 .
.代入求得DE="12" ,
四边形ABCD是平行四边形,又∵AE⊥BC,∴ AE⊥AD,
在Rt△AED中,由勾股定理可得AE=6.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
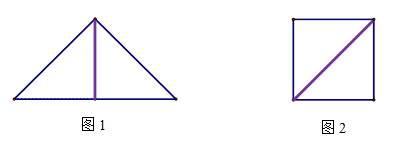
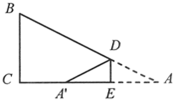
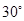 ,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;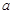 ,请直接写出每种拼法中最大三角形的斜边长.
,请直接写出每种拼法中最大三角形的斜边长.
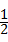 B、2 C、3 D、4
B、2 C、3 D、4