题目内容
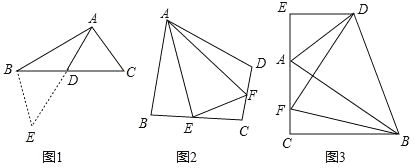
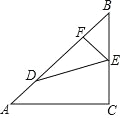
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
【答案】(1)证明见解析;(2)5.
【解析】
(1)连接 CD,利用 SAS 定理证明△ADC≌△BED,根据全等三角形的性质得到 DC=DE,∠DCA=∠EDB,根据等角的余角相等证明;
(2)作 DH⊥EC 于 H,根据等腰三角形的性质得到 EH=HC=![]() EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
解:(1)连接 CD,
∵AC=BC,∠ACB=90,
∴∠A=∠B=45°,
ADC 和△BED 中,
∴△ADC≌△BED(SAS),
∴DC=DE,∠DCA=∠EDB,
∴∠ECD=∠CED
∠DCA+∠ECD=∠EDB+∠FED=90°,
∴∠FED=∠ECD,
∴∠FED=∠CED;
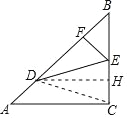
(2)作 DH⊥EC 于 H,
∵DC=DE,DH ⊥EC,
∴EH=HC= ![]() EC,∠EDH=∠CDH,
EC,∠EDH=∠CDH,
∵DH∥AC,
∴∠CDH=∠ACD,
∴∠FDE=∠FDH,又 EF⊥AB,EH⊥DH,
∴EF=EH=![]() EC,
EC,
∵∠BFE=90°,∠B=45°,
∴EF=BF= ![]() ,
,
∴EC=5,
故答案为:5.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目