��Ŀ����
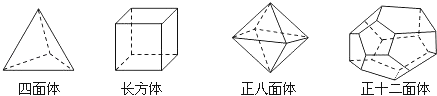
����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�������V����������F����������E��֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������۲����м��ּ�����ģ�ͣ�����������⣺

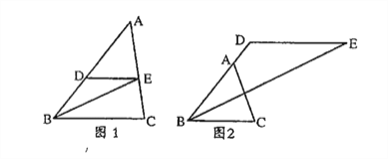
ͼ1 ͼ2
��̽����֪����ͼ1����1���������������ģ�ͣ���ɱ����еĿո�
������ | ��������V�� | ������F�� | ������E�� |
������ | 4 | 4 | |
������ | 8 | 6 | 12 |
�������� | 8 | 12 | |
��ʮ������ | 20 | 12 | 30 |
�㷢�ֶ�������V����������F����������E��֮����ڵĹ�ϵʽ���� ����
��2���������Ϲ�ϵʽ�����Ƿ����һ�������壬����16���棬50���⣬34�����㣿��д�����ɡ�
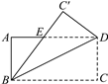
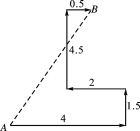
��ʵ��Ӧ�ã���ͼ2������һ����32��ڰ�Ƥ�ӷ�϶�������ɫ����������Σ���ɫ�����������Σ���
�����ǽ��ư�����һ�������壮
��1�����ɫ�����������x�飬���ɫ��������������32��x���飬��������һ��������ʱ������������ �������Ķ������� ����
��2�������Ƥ�Ͱ�Ƥ���ж��ٿ���
���𰸡���̽����֪����1��6,6��V+F��E=2��(2)�����ڣ�
��ʵ��Ӧ�á���1����![]() x+96������
x+96������![]() x+64����2�����������12�飬����������20�飮
x+64����2�����������12�飬����������20�飮
��������
̽����֪��1���۲�ͼ�μ��ɵó����ۣ��۲�ɵö�����+����-����=2��
��2�����루1���е�ʽ�Ӽ�����֤.
ʵ��Ӧ����1��ֱ������ŷ����ʽ����𰸣�
��2�����������֪�������еĵ�����ϵ�����ڰ�Ƥ��32��������Ϊÿ���Ƥ��3������ڱ�����һ�����Ժ�Ƥֻ�У�32-x���飬����Ƥ���б���Ϊ5x�飬���˽���ŷ����ʽ�з�����⼴�ɣ�
̽����֪��1���۲������Կ�����������+��������=2����ϵʽΪ��V+FE=2��
������ | ������(V) | ����(F) | ����(E) |
������ | 4 | 4 | 6 |
������ | 8 | 6 | 12 |
�������� | 6 | 8 | 12 |
��ʮ������ | 20 | 12 | 30 |
��2��������֪��V=34��F=16��E=50�������Ϲ�ϵʽ��V+FE=2.��û�������Ķ����.
ʵ��Ӧ����1�������������x�飬������������32x�飬
��F=32,E=5x+![]() =
= ![]() x+96
x+96
V=E��3��2=![]() +64
+64
��2������ŷ����ʽ�ã�V+FE=2��
��![]() x+64+32(
x+64+32(![]() x+96)=2��
x+96)=2��
��ã�x=12��32x=20��
���ԣ����������/span>12�飬����������20��.

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�