题目内容
已知:如图,AB是⊙O的直径,弦EF⊥AB于点D,如果EF=8,AD=2,则⊙O半径的长是 。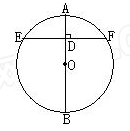

5
分析:连接OE,由题意得:OE=OA=R,ED=DF=4,再解Rt△ODE即可求得半径的值.
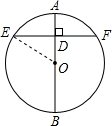
解:连接OE,如下图所示,则:
OE=OA=R,
∵AB是⊙O的直径,弦EF⊥AB,
∴ED=DF=4,
∵OD=OA-AD,
∴OD=R-2,
在Rt△ODE中,由勾股定理可得:
OE2=OD2+ED2,
∴R2=(R-2)2+42,
∴R=5.
故答案为:5.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
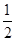
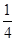
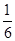
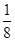

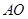 为12,母线
为12,母线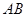 长为13,则该圆锥的侧面积等于( )
长为13,则该圆锥的侧面积等于( )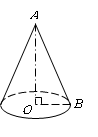

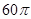
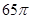
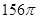
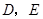 分别是半径
分别是半径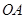 和
和 的中点
的中点
 CD=CE.
CD=CE.