Question

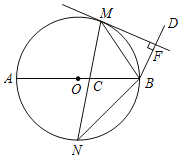
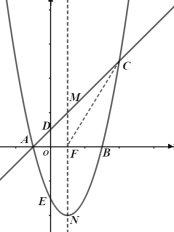
【题目】如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC＝∠D＝60°．

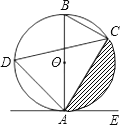
（1）求∠ABC的度数；

（2）求证：AE是⊙O的切线；

（3）当BC＝4时，求阴影部分的面积．

Answer 1

【答案】（1）60°；（2）见解析；（3）

【解析】

（1）根据∠ABC与∠D都是劣弧AC所对的圆周角，利用圆周角定理可证出∠ABC＝∠D＝60°；

（2）根据AB是⊙O的直径，利用直径所对的圆周角是直角得到∠ACB＝90°，结合∠ABC＝60°求得∠BAC＝30°，从而推出∠BAE＝90°，即OA⊥AE，可得AE是⊙O的切线；

（3）连接OC，作OF⊥AC，根据三角形中位线性质得出OF＝2，根据圆周角定理得出∠AOC＝120°，然后根据S阴影＝S扇形﹣S△AOC即可求得．

解：（1）∵∠ABC与∠D都是劣弧AC所对的圆周角，∠D＝60°，

∴∠ABC＝∠D＝60°；

（2）∵AB是⊙O的直径，∴∠ACB＝90°．

可得∠BAC＝90°﹣∠ABC＝30°，

∴∠BAE＝∠BAC+∠EAC＝30°+60°＝90°，

即BA⊥AE，得OA⊥AE，

又∵OA是⊙O的半径，

∴AE是⊙O的切线；

（3）连接OC，作OF⊥AC，

∴OF垂直平分AC，

∵OA＝OB，

∴OF＝BC＝2，

∵∠D＝60°，

∴∠AOC＝120°，∠ABC＝60°，

∴AC＝AB＝4，

∴S阴影＝S扇形﹣S△AOC＝．