题目内容
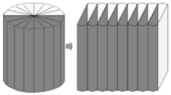
【题目】如图，把一个圆柱的底面平均分成若干个扇形，然后切开拼成一个近似的长方体，下列关于两个几何体的结论：①表面积不变；②表面积变大；③体积不变；④体积变大．其中结论正确的序号为________．
【答案】②③
【解析】
设圆柱的半径为r，高为h；根据圆柱的切割方法与拼组特点可知：拼成的长方体的长是圆柱底面周长的一半，即是πr；宽是半径的长度是r，高是原来圆柱的高h，由此利用长方体的表面积公式，代入数据即可解答．
设圆柱的半径为r，高为h；则拼成的长方体的长πr；宽是r，高是h，
①原来圆柱的表面积为：2πr2+2πrh；
拼成的长方体的表面积为：(πr×r+πr×h+h×r)×2=2πr2+2πrh+2hr
所以拼成的长方体的表面积比原来的圆柱的表面积变大了．
②原来圆柱的体积为：πr2h
拼成的长方体的体积为：πr×r×h=πr2h
所以拼成的长方体和圆柱的体积大小没变．
所以拼成的长方体的表面积比原来的圆柱的表面积变大了，但是体积没变；
故答案为：②③
练习册系列答案
相关题目
