题目内容
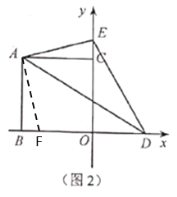
【题目】如图,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点,且点
上的动点,且点![]() 不与点
不与点![]() 、
、![]() 重合,
重合,![]() .
.

(1)如图1,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的周长;
的周长;
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,请猜想
,请猜想![]() 与
与![]() 之间的等量关系,并证明你的猜想.
之间的等量关系,并证明你的猜想.
【答案】(1)12;(2)2S1=36 +S2.
【解析】
(1)根据已知条件证得四边形ABOC是正方形,在点B左侧取点G,连接AG,使AG=AE,利用HL证得Rt△ABG≌Rt△ACE,得到∠GAB=∠EAC,GB=CE,再利用![]() 证得△GAD≌△EAD,得到DE=GB+BD,由此求得
证得△GAD≌△EAD,得到DE=GB+BD,由此求得![]() 的周长;
的周长;
(2) 在OB上取点F,使AF=AE,根据HL证明Rt△ABF≌Rt△ACE,得到∠FAE=∠ABC=90![]() ,再证明△ADE≌△ADF,利用面积相加关系得到四边形AEDF的面积=S△ACE+S四边形ACOF+S△ODE,根据三角形全等的性质得到2S△ADE=S正方形ABOC+S△ODE,即可得到2S△ADE=36 +S△ODE.
,再证明△ADE≌△ADF,利用面积相加关系得到四边形AEDF的面积=S△ACE+S四边形ACOF+S△ODE,根据三角形全等的性质得到2S△ADE=S正方形ABOC+S△ODE,即可得到2S△ADE=36 +S△ODE.
(1)∵点![]() 的坐标为
的坐标为![]() ,
,![]() 轴,
轴,![]() 轴,
轴,
∴AB=BO=AC=OC=6,
∴四边形ABOC是菱形,
∵∠BOC=90![]() ,
,
∴四边形ABOC是正方形,
在点B左侧取点G,连接AG,使AG=AE,
∵四边形ABOC是正方形,
∴AB=AC,∠ABG=∠ACE=90![]() ,
,
∴Rt△ABG≌Rt△ACE,
∴∠GAB=∠EAC,GB=CE,
∵∠BAE+∠EAC=90![]() ,
,
∴∠GAB+∠BAE=90![]() ,
,
即∠GAE=90![]() ,
,
∵![]()
∴∠GAD=![]() ,
,
又∵AD=AD,AG=AE,
∴△GAD≌△EAD,
∴DE=GD=GB+BD,
∴![]() 的周长=DE+OD+OE=GB+BD+OD+OE=OB+OC=6+6=12
的周长=DE+OD+OE=GB+BD+OD+OE=OB+OC=6+6=12

(2) 2S1=36 +S2,理由如下:
在OB上取点F,使AF=AE,
∵AB=AC,∠ABF=∠ACE=90![]() ,
,
∴Rt△ABF≌Rt△ACE,
∴∠BAF=∠CAE,
∴∠FAE=∠ABC=90![]() ,
,
∵∠DAE=45![]() ,
,
∴∠DAF=∠DAE=45![]() ,
,
∵AD=AD,
∴△ADE≌△ADF,
∵四边形AEDF的面积=S△ACE+S四边形ACOF+S△ODE,
∴2S△ADE=S正方形ABOC+S△ODE,
∴2S△ADE=36 +S△ODE
.即:2S1=36 +S2

【题目】某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
类别/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均数 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)将表格填写完整.
(2)求甲种计算器本周销售量的方差.
(3)已知乙种计算器本周销售量的方差为![]() ,本周哪种计算器的销售量比较稳定?说明理由.
,本周哪种计算器的销售量比较稳定?说明理由.